Теория балок Эйлера-Бернулли
Теория балок Эйлера-Бернулли (также известная как теория балок инженера или классическая теория балок) - это простой метод расчета изгиба балок при приложении нагрузки. Он применяется к небольшим прогибам (насколько что-то перемещается) балки без учета влияния сдвиговых деформаций. Поэтому его можно считать частным случаем теории балок Тимошенко. Впервые она была введена около 1750 года. Она приобрела популярность во время разработки Эйфелевой башни и колеса обозрения в конце 19 века. После этого она использовалась во многих инженерных областях, включая машиностроение и гражданское строительство. Хотя были разработаны другие передовые методы, теория балок Эйлера-Бернулли по-прежнему широко используется из-за своей простоты.
Вибрирующая стеклянная балка, демонстрирующая изгиб балок, который можно оценить с помощью теории балок Эйлера-Бернулли.
История
Леонгард Эйлер и Даниэль Бернулли были первыми, кто собрал теорию воедино в 1750 году. В то время наука и инженерия рассматривались иначе, чем сегодня. Математическим теориям, таким как теория балок Эйлера-Бернулли, не доверяли для практического инженерного использования. Мосты и здания продолжали проектировать теми же методами до конца 19 века. Именно тогда Эйфелева башня и колесо обозрения продемонстрировали действенность теории в более широком масштабе.
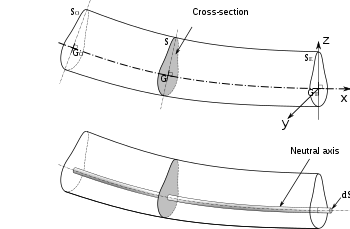
Чертеж поперечного сечения изогнутой балки с указанием нейтральной оси
Уравнение статической балки
Уравнение Эйлера-Бернулли описывает зависимость между прогибом балки и приложенной нагрузкой, как показано ниже:
d 2 d x 2 ( E I d 2 w d x 2 ) = q {\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}\right)=q\,} 
Где w ( x ) {\displaystyle w(x)} 
описывает прогиб балки в направлении z {\displaystyle z}
при некотором положении x {\displaystyle x} 
. q {\displaystyle q}
- распределенная нагрузка, другими словами сила на единицу длины (аналогично тому, как давление является силой на единицу площади); она может быть функцией x {\displaystyle x} , w {\displaystyle w} 
, или других переменных.
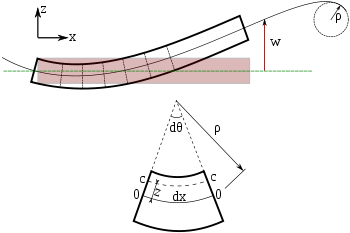
Изгиб балки Эйлера-Бернулли. Каждое сечение балки находится под углом 90 градусов к нейтральной оси.
Вопросы и ответы
В: Что такое теория балок Эйлера-Бернулли?
О: Теория балок Эйлера-Бернулли - это простой метод, используемый для расчета изгиба балок при приложении нагрузки, без учета влияния сдвиговых деформаций.
В: Когда была впервые представлена теория балок Эйлера-Бернулли?
О: Теория балок Эйлера-Бернулли была впервые представлена около 1750 года.
В: Использовалась ли теория балок Эйлера-Бернулли при разработке Эйфелевой башни и колеса обозрения?
О: Да, теория балок Эйлера-Бернулли приобрела популярность во время разработки Эйфелевой башни и колеса обозрения в конце 19 века.
В: В каких инженерных областях использовалась теория балок Эйлера-Бернулли?
О: Теория балок Эйлера-Бернулли использовалась во многих инженерных областях, включая машиностроение и гражданское строительство.
В: Широко ли теория балок Эйлера-Бернулли используется и сегодня?
О: Да, теория балок Эйлера-Бернулли все еще широко используется сегодня из-за своей простоты, несмотря на то, что были разработаны другие передовые методы.
В: К каким типам прогибов балки применима теория балок Эйлера-Бернулли?
О: Теория балок Эйлера-Бернулли применима к небольшим прогибам балки.
В: Учитывает ли теория балок Эйлера-Бернулли влияние сдвиговых деформаций?
О: Нет, теория балок Эйлера-Бернулли не учитывает эффекты сдвиговых деформаций.
