Theorema Egregium
Теорема Гаусса (лат. "Замечательная теорема") - важный результат дифференциальной геометрии, доказанный Карлом Фридрихом Гауссом. Теорема касается кривизны поверхностей. Теорема утверждает, что кривизна может быть определена только путем измерения углов, расстояний и их скоростей на поверхности. Нет необходимости говорить о том, каким именно образом поверхность вписана в окружающее трехмерное евклидово пространство. Другими словами, гауссова кривизна поверхности не меняется, если согнуть поверхность, не растягивая ее.
Гаусс представил теорему в таком виде (в переводе с латыни):
По этой причине формула предыдущей статьи сама собой приводит к замечательной теореме. Если криволинейную поверхность развить на любую другую поверхность, то мера кривизны в каждой точке остается неизменной.
Теорема "замечательна" тем, что исходное определение гауссовой кривизны напрямую использует положение поверхности в пространстве. Поэтому довольно удивительно, что результат не зависит от вложения, несмотря на все деформации изгиба и скручивания.
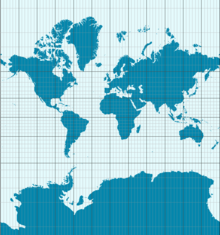
Следствием Теоремы Эгрегора является то, что Землю невозможно отобразить на карте без искажений. Проекция Меркатора, показанная здесь, сохраняет углы, но изменяет площадь. Например, Антарктида показана намного больше, чем она есть на самом деле.
Вопросы и ответы
В: Что такое "Теорема Гаусса" (Theorema Egregium)?
О: Эгрегориальная теорема Гаусса - это основной результат дифференциальной геометрии, касающийся кривизны поверхностей, доказанный Карлом Фридрихом Гауссом.
В: Как можно определить кривизну, согласно Теореме Гаусса об эгрегорах?
О: Согласно Теореме Гаусса (Theorema Egregium), кривизна может быть определена только путем измерения углов, расстояний и их скоростей на поверхности.
В: Необходимо ли для определения кривизны говорить о том, каким именно образом поверхность вписана в окружающее трехмерное евклидово пространство?
О: Нет, для определения кривизны в соответствии с Теоремой Гаусса не нужно говорить о том, каким именно образом поверхность вписана в окружающее трехмерное евклидово пространство.
В: Изменяется ли гауссова кривизна поверхности, если согнуть поверхность, не растягивая ее?
О: Нет, гауссова кривизна поверхности не изменится, если согнуть поверхность без растяжения, согласно Эгрегориальной Теореме Гаусса.
В: Кто представил теорему в таком виде?
О: Гаусс представил теорему именно таким образом.
В: Чем примечательна эта теорема?
О: Теорема "примечательна" тем, что в исходном определении гауссовой кривизны напрямую используется положение поверхности в пространстве. Поэтому весьма удивительно, что результат не зависит от вложения, несмотря на все деформации изгиба и скручивания.
В: В каком виде Гаусс представил теорему?
О: Гаусс представил теорему таким образом, что если криволинейную поверхность развить на любую другую поверхность, то мера кривизны в каждой точке остается неизменной.
искать