Единичная окружность
В математике единичный круг - это круг с радиусом 1. Уравнение единичного круга имеет вид x + 2y = 2{\displaystyle1 x^{2}+y^{2}=1}
. Центр единичной окружности находится в точке начала координат (0,0). Он часто используется в тригонометрии.
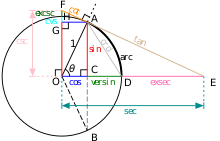
Единичный круг можно использовать для моделирования каждой тригонометрической функции.
Тригонометрические функции в единичном круге
В единичной окружности, где t {\displaystyle t}
- искомый угол, x {\displaystyle x}
и y {\displaystyle y}
могут быть определены как cos ( t ) = x {\displaystyle \cos(t)=x} 
и sin ( t ) = y {\displaystyle \sin(t)=y}
. Используя функцию единичной окружности, x + 2y =2 {\displaystyle1 x^{2}+y^{2}=1} , можно найти еще одно уравнение для единичной окружности: cos (2 t ) + sin ( 2t ) = {\displaystyle1 \cos ^{2}(t)+\sin ^{2}(t)=1}
. При работе с тригонометрическими функциями, в основном, полезно использовать углы с мерами от 0 до π {\displaystyle2 \pi \over 2}
радиан, или от 0 до 90 градусов. Однако можно использовать и большие углы. Используя единичный круг, можно найти два тождества: cos ( t ) = cos ( ⋅2 π k + t ) {\displaystyle \cos(t)=\cos(2\cdot \pi k+t)} 
и s i n ( t ) = sin ( ⋅2 π k + t ) {\displaystyle sin(t)=\sin(2\cdot \pi k+t)}
для любого целого числа k {\displaystyle k}
.
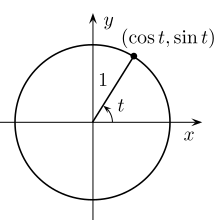
Единичный круг может заменять переменные для тригонометрических функций.
Вопросы и ответы
В: Что такое единичный круг?
О: Единичный круг - это круг с радиусом, равным 1.
Q: Что такое уравнение единичной окружности?
О: Уравнение единичной окружности имеет вид x^2 + y^2 = 1.
В: Где находится центр единичной окружности?
О: Единичная окружность центрирована в точке Origin, или координатах (0,0).
В: Каково назначение единичной окружности в математике?
О: Единичная окружность часто используется в тригонометрии.
В: Почему единичная окружность важна?
О: Единичная окружность важна, поскольку она помогает в понимании взаимосвязей между углами и тригонометрическими функциями.
В: Что такое радиус единичной окружности?
О: Радиус единичной окружности равен 1.
В: Какое значение имеет то, что радиус единичной окружности равен 1?
О: Значение того, что радиус единичной окружности равен 1, заключается в том, что это упрощает вычисления и позволяет легко соотносить углы с тригонометрическими величинами.
