Круг
Круг - это круглая, двумерная форма. Все точки на краю окружности находятся на одинаковом расстоянии от центра.
Радиус окружности - это линия от центра окружности до точки на стороне. Математики используют букву r для обозначения длины радиуса окружности. Центр окружности - это точка в самом центре.
Диаметр (что означает "весь путь через") окружности - это прямая линия, которая проходит с одной стороны на противоположную и прямо через центр окружности. Математики используют букву d для обозначения длины этой линии. Диаметр окружности равен двукратному радиусу (d равно 2 раза r).
d = 2 r {\displaystyle d =2 r}
Окружность (означающая "всю окружность") круга - это линия, проходящая вокруг центра круга. Математики используют букву C для обозначения длины этой линии.
Номер π (написанный как греческая буква pi) - очень полезное число. Оно представляет собой длину окружности, деленную на длину диаметра (π равно C, деленную на d). В качестве дроби число π равно примерно 22⁄7 или 335/113 (что ближе), а в качестве числа примерно 3.1415926535.
Область, a, внутри окружности равна радиусу, умноженному на себя, затем умноженному на π (a равна π умножить на r умножить на r).
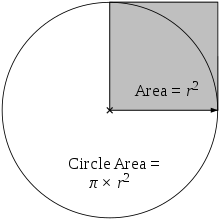
Площадь круга равна π, умноженной на площадь серого квадрата.

Круг
Вычисление π
π можно измерить, нарисовав большой круг, а затем измерив его диаметр (d) и окружность (C). Это происходит потому, что на сайте π окружность всегда умножается на диаметр.
π = C d {\displaystyle \pi ={\frac {C}{d}}}
π также может быть рассчитан только математическими методами. Большинство методов, используемых для расчета значения π, обладают желательными математическими свойствами. Однако их трудно понять, не зная тригонометрии и математического расчета. Однако некоторые методы достаточно просты, как, например, эта форма серии Грегори-Лейбница:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}-{\frac {4}{11}}\cdots}
Хотя этот ряд легко писать и вычислять, нелегко понять, почему он равен π. Легче понять подход - нарисовать воображаемый круг радиуса r, центрированный в начале. Тогда любая точка (x,y), расстояние d от начала меньше r, вычисленная по пифагорейской теореме, окажется внутри круга:
d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}}
Поиск набора точек внутри окружности позволяет оценить площадь окружности A. Например, используя целочисленные координаты для большой r. Так как площадь A окружности π умножается на квадрат радиуса, то π можно аппроксимировать:
π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}}
Связанные страницы
- Сфера
Вопросы и ответы
В: Что такое круг?
О: Круг - это круглая двухмерная фигура. Все точки на краю окружности находятся на одинаковом расстоянии от центра.
В: Что используют математики для обозначения длины радиуса окружности?
О: Математики используют букву r для обозначения длины радиуса окружности.
В: Что в окружностях пишется как О?
О: Центр окружности часто записывается как O.
В: Какова длина диаметра круга?
О: Диаметр (что означает "до конца") круга - это прямая линия, которая проходит от одной стороны к противоположной и прямо через центр круга. Он равен удвоенному радиусу (d равно 2 раза r).
В: Какую букву используют математики для обозначения окружности?
О: Математики используют букву C для обозначения окружности, что означает "все вокруг".
В: Как можно вычислить площадь внутри круга?
О: Площадь, A, внутри круга можно вычислить, умножив его радиус на себя, а затем умножив на ً (A равно ً умножить на r).
искать




