уравнение Юнга-Лапласа
В физике уравнение Янга-Лапласа (/ləˈplɑːs/) представляет собой нелинейное дифференциальное уравнение, описывающее разность капиллярного давления на границе раздела между двумя статическими жидкостями, такими как вода и воздух. Эта разница вызвана явлением поверхностного натяжения или натяжения стенок. Натяжение стенок может использоваться только для очень тонких стенок. Уравнение Юнга-Лапласа связывает разницу давлений с формой поверхности или стенки. Это очень важно при исследовании статических капиллярных поверхностей.
В физиологии это известно как закон Лапласа. Он используется для описания давления внутри полых органов.
Уравнение названо в честь Томаса Янга, разработавшего качественную теорию поверхностного натяжения в 1805 году, и Пьера-Симона Лапласа, завершившего математическое описание в следующем году. Иногда его также называют уравнением Янга-Лапласа-Гаусса: Карл Фридрих Гаусс объединил работу Юнга и Лапласа в 1830 году. Гаусс вывел как дифференциальное уравнение, так и граничные условия, используя принципы виртуальной работы Иоганна Бернулли.
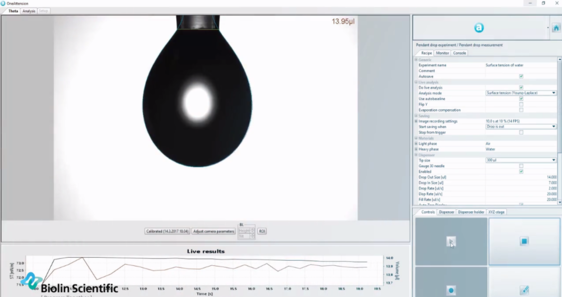
Оптические тензиометры используют уравнение Юнга-Лапласа для автоматического определения поверхностного натяжения жидкости на основе формы подвесной капли.
Вопросы и ответы
В: Что такое уравнение Янга-Лапласа?
О: Уравнение Янга-Лапласа - это нелинейное дифференциальное уравнение, которое описывает разность капиллярного давления на границе раздела двух статических жидкостей, таких как вода и воздух.
В: С чем это связано?
О: Оно связывает разность давлений с формой поверхности или стенки.
В: Кто разработал эту теорию?
О: Теория была разработана Томасом Янгом в 1805 году, а Пьер-Симон Лаплас завершил ее математическое описание в следующем году. Позже она была унифицирована Карлом Фридрихом Гауссом в 1830 году.
В: Как она используется в физиологии?
О: В физиологии он известен как закон Лапласа и используется для описания давления внутри полых органов.
В: Какое явление он объясняет?
О: Уравнение Юнга-Лапласа объясняет явление поверхностного натяжения или натяжения стенок.
В: Применимо ли натяжение стенок для толстых стенок? О: Нет, натяжение стенок может быть использовано только для очень тонких стенок.
искать