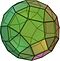
Архимедово тело
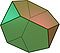
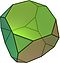
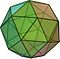
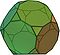
В геометрии архимедово тело - это выпуклая фигура, состоящая из многоугольников. Это многогранник, обладающий следующими свойствами:
- Каждая грань состоит из правильного многоугольника
- Все углы фигуры выглядят одинаково
- Форма не является ни платоновым твердым телом, ни призмой, ни антипризмой.
В зависимости от способа подсчета, таких фигур тринадцать или пятнадцать. Две из этих фигур имеют две версии, которые нельзя сделать конгруэнтными с помощью вращения. Архимедовы твердые тела названы в честь древнегреческого математика Архимеда, который, вероятно, открыл их в III веке до нашей эры. Труды Архимеда были утеряны, но Папп Александрийский обобщил их в IV веке. В эпоху Возрождения художники и математики ценили чистые формы и заново открыли все эти формы. Иоганн Кеплер, вероятно, завершил эти поиски около 1620 года.
Для построения архимедова тела требуется как минимум два разных многоугольника.
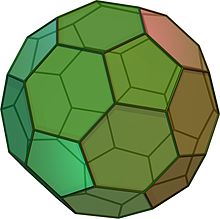
Усеченный икосаэдр похож на футбольный мяч. Он состоит из 12 равносторонних пятиугольников и 20 правильных шестиугольников. У него 60 вершин и 90 граней. Это архимедово твердое тело
Свойства
- Архимедовы твердые тела состоят из правильных многоугольников, поэтому все ребра имеют одинаковую длину.
- Все архимедовы твердые тела могут быть получены из платоновых твердых тел путем "срезания краев" платоновых твердых тел.
- Тип многоугольников, пересекающихся в углу ("вершине"), характеризует как архимедово, так и платоново твердое тело
Связь с платоновыми твердыми телами
Платоновы твердые тела можно превратить в архимедовы твердые тела, следуя ряду правил их построения.
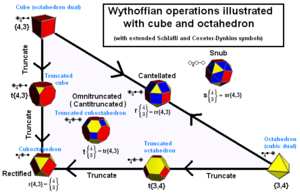
Архимедовы твердые тела могут быть построены как генераторные позиции в калейдоскопе
Перечисление архимедовых твердых тел
Ниже приводится список всех архимедовых твердых тел
| Изображение | Имя | Лица | Тип | Края | Вершины |
|
| Усеченный тетраэдр | 8 | 4 треугольника 4 шестиугольника | 18 | 12 |
|
| 14 | 8 треугольников 6 квадратов | 24 | 12 | |
|
| Усеченный куб | 14 | 8 треугольников 6 восьмиугольников | 36 | 24 |
|
| Усеченный октаэдр | 14 | 6 квадратов 8 шестиугольников | 36 | 24 |
|
| Ромбикубооктаэдр | 26 | 8 треугольников 18 квадратов | 48 | 24 |
|
| Усеченный кубооктаэдр | 26 | 12 квадрата 8 шестиугольников 6 восьмиугольников | 72 | 48 |
|
| Куб (2 зеркальные версии) | 38 | 32 треугольника 6 квадратов | 60 | 24 |
|
| Икосидодекаэдр | 32 | 20 треугольников 12 пятиугольников | 60 | 30 |
|
| Усеченный додекаэдр | 32 | 20 треугольников 12 декагонов | 90 | 60 |
|
| Усеченный икосаэдр | 32 | 12 пятиугольников 20 шестиугольников | 90 | 60 |
|
| Ромбикосидодекаэдр | 62 | 20 треугольников30 квадратов12 | 120 | 60 |
|
| Усеченный икосидодекаэдр | 62 | 30 квадратов 20 шестиугольников 12 декагонов | 180 | 120 |
|
| Додекаэдр (2 зеркальные версии) | 92 | 80 треугольников 12 пятиугольников | 150 | 60 |
Вопросы и ответы
В: Что такое архимедово твердое тело?
О: Архимедово тело - это выпуклая фигура из многоугольников, каждая грань которой является правильным многоугольником, все углы выглядят одинаково, и которая не является платоновым телом, призмой или антипризмой.
В: Сколько существует архимедовых твердых тел?
О: В зависимости от того, как их считать, существует тринадцать или пятнадцать архимедовых твердых тел.
В: Кто открыл архимедовы твердые тела?
О: Архимедовы твердые тела названы в честь древнегреческого математика Архимеда, который, вероятно, открыл их в 3 веке до н.э.
В: Что сделал Папп Александрийский с трудами Архимеда?
О: Папп Александрийский обобщил труды Архимеда об Архимедовых твердых телах в 4 веке.
В: Почему художники и математики заново открыли архимедовы твердые тела в эпоху Возрождения?
О: В эпоху Возрождения художники и математики ценили чистые формы, а архимедовы твердые тела считались чистыми формами.
В: Когда Иоганн Кеплер завершил поиск всех архимедовых твердых тел?
О: Иоганн Кеплер, вероятно, завершил поиск всех архимедовых твердых тел около 1620 года.
В: Что необходимо для построения архимедова твердого тела?
О: Для построения архимедова твердого тела требуется как минимум два различных многоугольника.
искать