Вероятностное пространство
Вероятностное пространство - это математическая модель, используемая для описания научных экспериментов Вероятностное пространство состоит из трех частей:
- Образец пространства, в котором перечислены все возможные результаты
- Множество событий. Каждое событие ассоциируется с нулевыми или более результатами
- Функция, которая присваивает вероятности каждому событию.
Результат - результат единичного выполнения модели. Поскольку отдельные результаты могут иметь мало практического применения, для характеристики групп результатов используются более сложные события. Сборник всех таких событий представляет собой σ-algebra F {\displaystyle \scriptstyle {\mathcal {F}}}. 
. Наконец, необходимо указывать вероятность наступления каждого события. Это делается с помощью функции измерения вероятности, P.
Как только пространство вероятностей установлено, предполагается, что "природа" делает свой ход и выбирает единственный результат, ω, из пространства выборки Ω. Все события в F {\displaystyle \scriptstyle {\mathcal {F}}, которые содержат выбранный результат ω (напомним, что каждое событие является подмножеством Ω), считаются "произошедшими". Выбор по природе осуществляется таким образом, что если эксперимент повторить бесконечное число раз, то относительные частоты наступления каждого из событий будут совпадать с вероятностями, предписанными функцией P.
Выдающийся советский математик Андрей Колмогоров в 1930-е годы ввел понятие пространства вероятностей вместе с другими аксиомами вероятности.
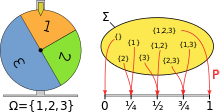
Моделирование колеса фортуны с использованием вероятностного пространства
Вопросы и ответы
В: Что такое вероятностное пространство?
О: Вероятностное пространство - это математическая модель, используемая для описания научных экспериментов. Оно состоит из трех частей: пространства выборок, в котором перечислены все возможные исходы, набора событий, которые связывают ноль или более исходов, и функции, которая присваивает вероятности каждому событию.
В: Из чего состоит пространство выборок?
О: Пространство выборки состоит из всех возможных исходов, часто записываемых как Ω {\displaystyle \Omega } , а исход как ω {\displaystyle \omega } .
В: Что такое исход?
О: Результат - это результат одного выполнения модели.
В: Для чего используются события в вероятностных пространствах?
О: События используются для характеристики групп исходов, поскольку отдельные исходы могут иметь мало практической пользы. Коллекция всех таких событий называется σ-алгеброй, иногда записывается как F {\displaystyle {\mathcal {F}}}.
В: Как присваиваются вероятности каждому событию?
О: Вероятности присваиваются каждому событию с помощью функции меры вероятности P.
В: Кто ввел понятие вероятностных пространств? О: Выдающийся советский математик Андрей Колмогоров ввел понятие вероятностных пространств вместе с другими аксиомами вероятности в 1930-х годах.
