Функция (математика)
В математике функция - это математический объект, который производит на выходе, когда ему дается вход - это может быть число, вектор или что угодно, что может существовать внутри множества вещей.
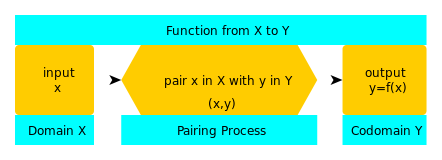
Таким образом, функция похожа на машину, которая принимает значения x и возвращает выходные y. Набор всех значений, которые может иметь x, называется доменом. Множество, которое содержит каждое значение, которое может иметь y, называется кодоменом.
Если такое случается, мы говорим, что y - это функция x, и пишем y =f(x). f - это имя функции, и пишем f : X → Y {\displaystyle f:X\to Y}. 
(функция от X до Y) для представления трех частей функции: домена (x), кодомена (y) и процесса сопряжения (стрелка).
Пример функции f(x)=x+1 В качестве входного значения дается натуральное число x {\displaystyle x}
(0,1,2,3...) и получается натуральное число y {\displaystyle y}. 
, то есть x {\displaystyle x} +1 (1,2,3,4...) Идея функции была настроена так, чтобы охватить всевозможные возможности. Функция не обязательно должна быть уравнением. Основная идея заключается в том, что входы и выходы каким-то образом спарены, даже если процесс очень сложный.
Метафоры
Таблицы
Входы и выходы могут быть помещены в таблицу, как на картинке; это легко сделать, если данных не слишком много.
Графики
На рисунке видно, что и 2, и 3 были сопряжены с c; это недопустимо в другом направлении, 2 не могли вывести c и d, на каждом входе может быть только один выход. Все f ( x ) {\displaystyle f(x)} 
(c и d на картинке) обычно называются набором изображений f {\displaystyle f}
, а набор изображений может быть всем кодоменом или нет. Можно сказать, что подмножеством А кодомена с набором изображений является f(A). Если входы и выходы имеют порядок, то их легко построить на графике:
Таким образом, изображение попадает на изображение множества А. Это сделает так, что и 2, и 3 не разрешается объединять в пары в другом направлении, даже можно сделать между кодоменами или нет. Можно сделать вывод, что подмножеством А кодомена является изображение множества F(A).
История
В 1690-х годах ГотфридЛейбниц и Иоганн Бернулли использовали функцию слова в буквах между ними, так что современное понятие начиналось одновременно с исчислением.
В 1748 году Леонхард Эйлер дал: "Функция переменной величины - это аналитическое выражение, составленное каким-либо образом из переменной величины и чисел или из постоянных величин", а затем в 1755 году: "Если одни величины настолько зависят от других величин, что при изменении последних происходит изменение первых, то первые величины называются функциями вторых". Это определение применяется достаточно широко и включает в себя все способы, с помощью которых одна величина может быть определена другой. Если, следовательно, х обозначает переменную величину, то все величины, которые каким-либо образом зависят от х или определяются им, называются функциями х.", что очень современно.
Обычно Дирихлету приписывают версию, использовавшуюся в школах до второй половины 20-го века: "y - это функция переменной x, определенной на интервале a < x < b, если каждому значению переменной x в этом интервале соответствует определенное значение переменной y. Также не имеет значения, каким образом это соответствие установлено".
В 1939 году Бурбаки обобщил определение Дирихлета и дал теоретическую версию определения как соответствия между входами и выходами; это определение использовалось в школах примерно с 1960 года.
Наконец, в 1970 году Бурбаки дал современное определение как тройное f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 
с F ⊂ X × Y , ( x , f ( x ) ) ∈ F {\displaystyle F\subset X\times Y,(x,f(x))\in F}
(т.е. f : X → Y {\displaystyle f:X\to Y} и F = {( x , f( x) ) | x ∈ Х , f ( x ) ∈ Y } {\displaystyle F={(x,f(x))|x\in X,f(x)\in Y}} 
).
Виды функций
- Элементарные функции - Функции, которые обычно изучаются в школе: дроби, квадратные корни, синусоидальные, косинусоидальные и касательные функции и некоторые другие функции.
- Неэлементарные функции - Большинство из них не используют операции, которым мы не учимся в школе (например, + или -, или полномочия). Многие интегралы являются неэлементарными.
- Обратные функции - Функции, которые отменяют другую функцию. Например: если F(x) противоположна f(x)=y, то F(y)=x. Не все функции имеют обратные вызовы.
- Специальные функции: Функции, у которых есть имена. Например: синус, косинус и тангенс. Такие функции, как f(x)=3x (трижды x) не называются специальными функциями. Они могут быть элементарными, неэлементарными или обратными.
Вопросы и ответы
В: Что такое функция в математике?
О: Функция в математике - это объект, который производит выход, когда ему дается вход, который может быть числом, вектором или чем угодно, что может существовать внутри множества вещей.
В: Какие два множества связаны с функциями?
О: Множество всех значений, которые может иметь x, называется доменом, а множество, содержащее все значения, которые может иметь y, называется кодоменом.
В: Как часто обозначают функции?
О: Функции часто обозначаются курсивными буквами, например, f, g, h.
В: Как мы представляем функцию?
О: Мы представляем функцию, записывая y = f(x), где f - имя функции, а f : X → Y (функция от X к Y) обозначает три части функции - область (X), кодомен (Y) и процесс сопряжения (стрелка).
В: Можете ли Вы привести пример функции?
О: Примером функции является f(x) = x + 1. На вход подается натуральное число x и получается натуральное число y, которое равно x + 1. Например, если на вход функции f подать 3, то на выходе получится 4.
В: Должна ли каждая функция быть уравнением?
О: Нет, не каждая функция должна быть уравнением. Основная идея функций заключается в том, что входы и выходы как-то сопрягаются - даже если это может быть очень сложно.
