Вектор (геометрия)

Примеры векторов

• Джон идет на север 20 метров. Направление "север" вместе с расстоянием "20 метров" - это вектор.
• Яблоко падает вниз со скоростью 10 метров в секунду. Направление "вниз" в сочетании со скоростью "10 метров в секунду" является вектором. Такой вектор также называется скоростью.

Примеры скаляров

• Расстояние между двумя местами составляет 10 километров. Это расстояние не является вектором, так как не содержит направления.
• Количество фруктов в коробке не является вектором.
• Указание человека не является вектором, потому что существует только направление. Нет величины (расстояние от пальца человека до здания, например).
• Длина объекта.
• Автомобиль едет со скоростью 100 километров в час. Это не описывает вектор, так как здесь есть только величина, но нет направления.

Другие примеры векторов

• Перемещение - это вектор. Перемещение - это расстояние, на которое что-то перемещается в определенном направлении. Мера расстояния сама по себе является скаляром.
• Сила, включающая направление, является вектором.
• Скорость - это вектор, потому что это скорость в определенном направлении.
• Ускорение - это скорость изменения скорости. Объект ускоряется, если он меняет скорость или направление.

Как добавить векторы

Добавление векторов на бумаге методом "голова к хвосту

Метод сложения векторов "от головы до хвоста" полезен для оценки на бумаге результата сложения двух векторов. Для этого:

• Каждый вектор рисуется в виде стрелки с длиной за ней, где каждая единица длины на бумаге представляет собой определенную величину вектора.
• Нарисуйте следующий вектор так, чтобы хвост (конец) второго вектора находился в голове (передней части) первого вектора.
• Повторите для всех последующих векторов: Нарисуйте хвост следующего вектора в голове предыдущего.
• Проведите линию от хвоста первого вектора до головы последнего вектора - это результирующая (сумма) всех векторов.

Это называется методом "голова к хвосту", потому что каждая голова предыдущего вектора ведет к хвосту следующего.

Использование формы компонента

^{[нуждается в объяснении}

Использование компонентной формы для сложения двух векторов буквально означает сложение компонент векторов для создания нового вектора. Например, пусть a и b - два двумерных вектора. Эти векторы могут быть записаны в терминах их компонент.

a = ( a x , a y ) {\displaystyle \mathbf {a} =(a_{x},a_{y})}

b = ( b x , b y ) {\displaystyle \mathbf {b} =(b_{x},b_{y})}

Предположим, что c - сумма этих двух векторов, так что c = a + b. Это означает, что c = ( a x + b x , a y + b y ) {\displaystyle \mathbf {c} =(a_{x}+b_{x},a_{y}+b_{y})} .

Приведем пример сложения двух векторов, используя их компонентные формы.

a = ( , 3-1 ) {\displaystyle \mathbf {a} =(3,-1)}

b = ( ,2 ) 2{\displaystyle \mathbf {b} =(2,2)}

c = a + b {\displaystyle \mathbf {c} =\mathbf {a} +\mathbf {b} }

= ( a x + b x , a y + b y ) {\displaystyle =(a_{x}+b_{x},a_{y}+b_{y})}

= ( + 3, 2-1 + ) 2{\displaystyle =(3+2,-1+2)}

= ( , 5) 1{\displaystyle =(5,1)}

Этот метод работает для всех векторов, а не только для двумерных.

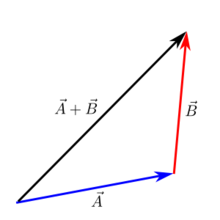
Дополнение от головы до хвоста

Как перемножать векторы

Использование точечного произведения

Точечное произведение - это один из методов умножения векторов. В результате получается скаляр. В нем используется компонентная форма:

a = ( ,2 ) 3b = ( , 1) 4a ⋅ b = ( ,2 )3 ⋅ ( , 1) 4= ( ⋅21 ) + ( ⋅34 ) = +2 = 12{\displaystyle {\begin{aligned}\mathbf {a} =(2,3)\\\\mathbf {b} =(1,414)\\\mathbf {a} \cdot \mathbf {b} =(2,3)\cdot (1,4)\\\=(2\cdot 1)+(3\cdot 4)\\\\=2+12=14\end{aligned}}}}

Использование перекрестного продукта

Кросс-продукт - это еще один метод умножения векторов. В результате получается другой вектор. Используя компонентную форму:

a × b = | a | | | b | sin ( θ ) n {\displaystyle \mathbf {a} \times \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\sin(\theta )\mathbf {n} }

Здесь | a | {\displaystyle |\mathbf {a} |} означает длину a {\displaystyle \mathbf {a} } и n {\displaystyle \mathbf {n} } - единичный вектор, расположенный под прямым углом к a {\displaystyle \mathbf {a} } и b {\displaystyle \mathbf {b} } .

Умножение на скаляр

Чтобы умножить вектор на скаляр (обычное число), нужно умножить число на каждый компонент вектора:

c x = ( c x ,1 c x ,2 . . . , c x n ) {\displaystyle c\,\mathbf {x} =(c\,x_{1},c\,x_{2},...,c\,x_{n})}

В качестве примера можно привести

c = x5 = ( ,3 )4 c x = ( ⋅53 , ⋅54 ) = ( , 15) 20{\displaystyle {\begin{aligned}c=5\\\\\mathbf {x} =(3,4)\\\c\,\mathbf {x} =(5\cdot 3,5\cdot 4)\\\=(15,20)\end{aligned}}}}.

Похожие страницы

• Векторная графика
• Векторное поле