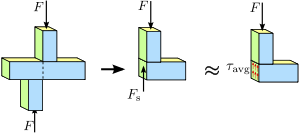Механическое напряжение
Нагрузка - это сила на единицу площади на теле, которая имеет тенденцию вызывать изменение его формы.
Нагрузка - это мера внутренних сил в теле между его частицами. Эти внутренние силы являются реакцией на внешние силы, приложенные к телу, которые заставляют его отделяться, сжиматься или скользить. Внешние силы - это либо поверхностные силы, либо силы тела. Нагрузка - это средняя сила на единицу площади, которую частица тела прилагает к соседней частице через воображаемую поверхность, которая их разделяет.
Формула одноосного нормального стресса:
σ = F A {\displaystyle {\sigma }={\frac {F}{A}}}
где σ - напряжение, F - сила, а A - площадь поверхности.
В единицах СИ сила измеряется в тритонах, а площадь - в квадратных метрах. Это означает, что напряжение составляет тритона на квадратный метр, или Н/м2. Однако напряжение имеет свою собственную единицу СИ, называемую паскаль. 1 паскаль (символ Pa) равен 1 Н/м2. В имперских единицах напряжения измеряется в фунтах силы на квадратный дюйм, который часто укорачивается до "psi". Размер напряжения тот же, что и давление.
В механике континуума загруженное деформируемое тело ведет себя как континуум. Таким образом, эти внутренние силы непрерывно распределяются в пределах объема материального тела. (Это означает, что распределение напряжений в теле выражается в виде кусочно-непрерывной функции пространства и времени). Эти силы вызывают деформацию формы тела. Деформация может привести к постоянному изменению формы или структурному разрушению, если материал недостаточно прочен.
Некоторые модели механики континуума рассматривают силу как нечто, что может измениться. Другие модели смотрят на деформацию материи и твердых тел, потому что характеристики материи и твердых тел трехмерны. Каждый подход может дать различные результаты. Классические модели механики континуума предполагают среднюю силу и не включают должным образом "геометрические факторы". (Геометрия тела может быть важна для того, как распределяется напряжение и как энергия накапливается при приложении внешней силы).
Рисунок 1.4 Стресс сдвига в призматической полосе. Распределение напряжений или сил в поперечном сечении стержня не обязательно является равномерным. Тем не менее, среднее напряжение сдвига τ a v g {\displaystyle \tau _{\mathrm {avg}. }\,\! } 
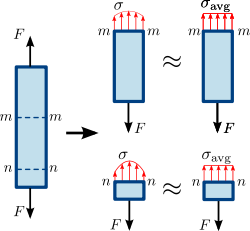
Рисунок 1.3 Нормальное напряжение в призматической (прямой член равномерной площади поперечного сечения) полосе. Распределение напряжений или сил в поперечном сечении бара не обязательно является равномерным. Однако среднее нормальное напряжение σ a v g {\displaystyle \sigma _{\mathrm {avg}. }\,\! } 
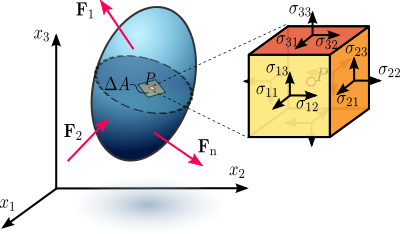
Рисунок 1.1 Нагрузка в нагруженном деформируемом материале в виде континуума.
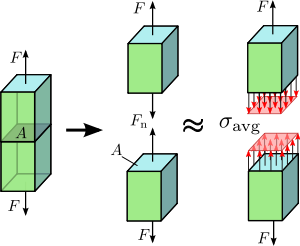
Рисунок 1.2 Осевое напряжение в призматической балке, нагруженной по оси.
напряжение сдвига
Дополнительная информация: напряжение сдвига
Простые напряжения
В некоторых ситуациях напряжение внутри объекта может быть описано одним числом или одним вектором (числом и направлением). Три такие простые стрессовые ситуации - это одноосное нормальное напряжение, простое напряжение сдвига и изотропное нормальное напряжение.
одноосный нормальный стресс
Напряжение при растяжении (или растяжение) - это напряженное состояние, приводящее к расширению, т.е. длина материала имеет тенденцию увеличиваться в направлении растяжения. Объем материала остается постоянным. Когда к телу прилагаются равные и противоположные силы, то возникающее в результате этой силы напряжение называется растягивающим напряжением.
Поэтому в одноосном материале длина увеличивается в направлении растягивающих напряжений, а два других направления уменьшаются в размерах. При одноосном способе растяжения растягивающее напряжение индуцируется растягивающими силами. Напряжение при растяжении является противоположностью напряжениюпри сжатии.
Конструктивные элементы в прямом натяжении - это канаты, грунтовые анкеры и гвозди, болты и т.д. Балки, подверженные изгибающим моментам, могут включать в себя растягивающее напряжение, а также сжимающее напряжение и/или напряжение сдвига.
Напряжение при растяжении может быть увеличено до достижения предела прочности при растяжении, а именно до предельного состояния напряжения.
Стресс в одномерных телах
Все реальные объекты занимают трехмерное пространство. Однако, если два измерения очень большие или очень маленькие по сравнению с другими, то объект может быть смоделирован как одномерный. Это упрощает математическое моделирование объекта. К одномерным объектам относятся кусок проволоки, нагруженный концами и рассматриваемый со стороны, и металлический лист, нагруженный лицевой стороной и рассматриваемый вблизи и сквозь поперечное сечение.
Связанные страницы
- Напряжение
- Bending
Вопросы и ответы
В: Что такое стресс?
О: Стресс - это сила, действующая на единицу площади тела и вызывающая изменение его формы. Оно является мерой внутренних сил в теле между его частицами и представляет собой среднюю силу на единицу площади, которую частица тела оказывает на соседнюю частицу через воображаемую поверхность, разделяющую их.
В: Как внешние силы влияют на напряжение?
О: Внешние силы - это либо поверхностные силы, либо силы тела, и они вызывают деформацию формы тела, которая может привести к постоянному изменению формы или разрушению структуры, если материал недостаточно прочен.
В: Какова формула для одноосного нормального напряжения?
О: Формула для одноосного нормального напряжения имеет вид σ = F/A, где σ - напряжение, F - сила, а A - площадь поверхности. В единицах СИ сила измеряется в ньютонах, а площадь - в квадратных метрах, поэтому напряжение будет равно ньютонам на квадратный метр (Н/м2). Однако существует собственная единица СИ для напряжения, называемая паскаль (Па), которая равна 1 Н/м2. В имперских единицах оно измеряется в фунтах силы на квадратный дюйм (psi).
В: Что механика сплошной среды предполагает относительно силы?
О: Классические модели механики сплошной среды предполагают среднюю силу и не учитывают должным образом геометрические факторы - это означает, что они не принимают во внимание, как геометрия влияет на накопление энергии при приложении внешней силы.
В: Как разные модели могут давать разные результаты при рассмотрении деформации материи и твердых тел?
О: Различные модели по-разному рассматривают деформацию материи и твердых тел, поскольку характеристики материи и твердых тел трехмерны - поэтому каждый подход учитывает различные аспекты, что может привести к различным результатам.
В: Как механика сплошной среды относится к нагруженным деформируемым телам?
О: Механика сплошных сред рассматривает нагруженные деформируемые тела как континуумы - это означает, что внутренние силы распределяются непрерывно в объеме материального тела, а не концентрируются в определенных точках, как в классических моделях.
искать