Цилиндр
Цилиндр - это одна из самых простых криволинейных геометрических фигур, поверхность которой образована точками, находящимися на фиксированном расстоянии от заданного отрезка прямой, называемого осью цилиндра. Эту форму можно представить как круглую призму. И поверхность, и твердая форма, образованная внутри, могут быть названы цилиндром. Площадь поверхности и объем цилиндра известны с древних времен.
В дифференциальной геометрии цилиндр определяется в более широком смысле как любая линейчатая поверхность, которую охватывает однопараметрическое семейство параллельных линий. Цилиндр, поперечное сечение которого представляет собой эллипс, параболу или гиперболу, называется эллиптическим, параболическим или гиперболическим цилиндром соответственно.
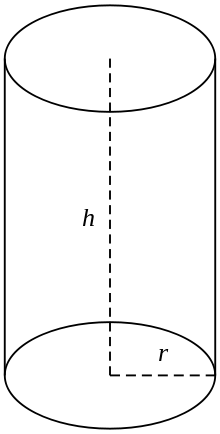
Правильный круговой цилиндр
Общее использование
В обиходе под цилиндром понимается конечное сечение правильного кругового цилиндра, т.е. цилиндра с образующими линиями, перпендикулярными основаниям, концы которого замкнуты и образуют две круговые поверхности, как на рисунке (справа). Если цилиндр имеет радиус r и длину (высоту) h, то его объем определяется как:
V = πrh2
а площадь его поверхности составляет:
- площадь вершины (πr2) +
- площадь дна (πr2) +
- область бока (2πrh).
Таким образом, без учета верхней или нижней части (боковая площадь), площадь поверхности составляет:
A = 2πrh.
Сверху и снизу площадь поверхности составляет:
A = 2πr2 + 2πrh = 2πr(r + h).
При заданном объеме цилиндр с наименьшей площадью поверхности имеет h = 2r. Для данной площади поверхности цилиндр с наибольшим объемом имеет h = 2r, т.е. цилиндр помещается в куб (высота = диаметр).
Том
Имея правильный круговой цилиндр высотой h единиц и основанием радиуса r единиц с координатными осями, выбранными так, что начало координат находится в центре одного основания, а высота измеряется вдоль положительной оси x. Сечение плоскости на расстоянии x единиц от начала координат имеет площадь A(x) квадратных единиц, где
A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}}
или
A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}}
Элементом объема, является правильный цилиндр с площадью основания Awi квадратных единиц и толщиной Δxi единиц. Таким образом, если V кубических единиц - объем правого кругового цилиндра, то по суммам Римана,
V o l u m e o f c y l i n d e r = lim | | | | Δ → | 0| ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {объем\;из\;цилиндр} =\lim _{||\Delta \to 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫0 h A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫0 h π r d 2y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Используя цилиндрические координаты, объем может быть вычислен интегрированием по
= ∫0 h ∫02 π ∫ 0r s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Цилиндрическое сечение
Цилиндрические сечения - это пересечения цилиндров с плоскостями. Для правильного кругового цилиндра существует четыре варианта. Плоскость, касательная к цилиндру, пересекает цилиндр по одной прямой. Двигаясь параллельно самой себе, плоскость либо не пересекает цилиндр, либо пересекает его по двум параллельным прямым. Все остальные плоскости пересекают цилиндр по эллипсу или, если они перпендикулярны оси цилиндра, по окружности.
Другие типы цилиндров
Эллиптический цилиндр, или цилиндроид, - это квадрическая поверхность со следующим уравнением в декартовых координатах:
( x a ) +2 ( y b ) = 21. {\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1.}
Это уравнение для эллиптического цилиндра, обобщения обычного кругового цилиндра (a = b). Еще более общим является обобщенный цилиндр: его поперечное сечение может быть любой кривой.
Цилиндр является вырожденным квадриком, поскольку по крайней мере одна из координат (в данном случае z) не фигурирует в уравнении.
У наклонного цилиндра верхняя и нижняя поверхности смещены относительно друг друга.
Существуют и другие, более необычные типы цилиндров. Это воображаемые эллиптические цилиндры:
( x a ) +2 ( y b ) =2 - 1{\displaystyle \left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=-1}
гиперболический цилиндр:
( x a )2 - ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}\right)^{2}-\left({\frac {y}{b}}\right)^{2}=1}
и параболический цилиндр:
x +2 a 2y = 0. {\displaystyle x^{2}+2ay=0.\,}

Эллиптический цилиндр

В проективной геометрии цилиндр - это просто конус, вершина которого находится на бесконечности, что визуально соответствует тому, что цилиндр в перспективе кажется конусом в сторону неба.
Проективная геометрия
В проективной геометрии цилиндр - это просто конус, вершина которого находится на бесконечности.
Это полезно при определении вырожденных коник, которые требуют рассмотрения цилиндрических коник.
Вопросы и ответы
В: Что такое цилиндр?
О: Цилиндр - это трехмерная геометрическая фигура, поверхность которой образована точками, расположенными на фиксированном расстоянии от заданного отрезка прямой, называемого осью цилиндра. Его можно представить себе как круглую призму, и как поверхность, так и твердую форму, образованную внутри, можно назвать цилиндром.
В: Как давно люди знают о площади поверхности и объеме цилиндров?
О: Площадь поверхности и объем цилиндров известны с древних времен.
В: Что такое эллиптический, параболический и гиперболический цилиндры?
О: Эллиптические, параболические и гиперболические цилиндры - это цилиндры, поперечное сечение которых представляет собой эллипс, параболу или гиперболу соответственно.
В: Как определяется цилиндр в дифференциальной геометрии?
О: В дифференциальной геометрии цилиндр определяется более широко как линейчатая поверхность, которую охватывает однопараметрическое семейство параллельных линий.
В: Что означает для чего-то быть "управляемым"?
О: Быть "правильным" означает, что на нем тем или иным способом нарисованы прямые линии.
В: Существует ли только один тип цилиндра?
О: Нет, существует много различных типов цилиндров, таких как эллиптический, параболический и гиперболический цилиндры, которые имеют различные поперечные сечения.
искать










