Размерность пространства
Размеры - это то, как мы видим, измеряем и переживаем наш мир. Используя вверх и вниз, вправо и влево, назад и вперед, горячий и холодный, как тяжелый и как долго, а также более продвинутые концепции из математики и физики. Один из способов определить измерение - это посмотреть на степень свободы или на то, как объект может перемещаться в определенном пространстве. Существуют различные концепции или способы использования термина "измерение", а также различные определения. Не существует определения, которое могло бы удовлетворить все понятия.
В векторном пространстве (вектор - открытая конечная линия) размерность равна кардинальности или числу направлений векторов или линий. Оно также равно числу наибольшей группы прямых направлений этого пространства. "Нормальные" объекты в повседневной жизни задаются тремя измерениями, которые обычно называют длиной, шириной и глубиной. Математики называют это понятие евклидовым пространством.
Размеры могут быть использованы и для измерения положения. Расстояние до позиции от места старта может быть измерено по длине, ширине и высоте. Эти расстояния являются мерой положения.
Иногда четвертое (4D) измерение - время - используется для отображения положения события во времени и пространстве.
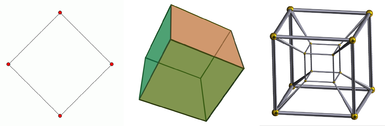
Слева направо, квадрат, куб и тессеракт. Квадрат - 2-х мерный объект, куб - 3-х мерный объект, а тессеракт - 4-х мерный объект. 1-мерный объект - это всего лишь линия. Проекция куба дается, так как он просматривается на двухмерном экране. То же самое относится и к тессеракте, которая дополнительно может быть показана в виде проекции даже в трехмерном пространстве.

Диаграмма первых четырех пространственных измерений.
Другие размеры
В современной науке люди используют другие измерения. Такие размеры, как температура и вес, могут использоваться для отображения положения чего-либо в менее простых пространствах. Ученые изучают эти размеры с помощью размерного анализа.
Математики также используют размеры. В математике измерения носят более общий характер. Измерения в математике могут не измерять вещи в мире. Правила арифметики с измерениями в математике могут отличаться от обычных правил арифметики.
Размеры и векторы
Векторы используются для отображения расстояний и направлений. Векторы часто используются в инженерных и естественных науках, а иногда и в математике.
Вектор - это список чисел. Для каждого измерения есть по одному числу. Для векторов существуют правила арифметики.
Например, если Джейн хочет знать позицию Салли, Салли может дать Джейн вектор, чтобы показать позицию. Если Джейн и Салли в мире, то есть три измерения. Поэтому Салли дает Джейн список из трех чисел, чтобы показать ее положение. Три числа в векторе, который Салли дает Джейн, могут быть:
- Расстояние Салли к северу от Джейн
- Расстояние Салли к востоку от Джейн
- рост Салли выше Джейн
Вопросы и ответы
В: Что такое измерение?
О: Измерение - это способ измерения, видения и восприятия мира с помощью таких понятий, как верх и низ, право и лево, зад и перед, горячее и холодное, тяжесть и длина. Его также можно определить как степени свободы или то, как объект может двигаться в определенном пространстве.
В: Как математики определяют евклидово пространство?
О: Математики определяют евклидово пространство как заданное тремя измерениями, которые обычно называются длиной, шириной и глубиной.
В: Каково количество векторов в векторном пространстве?
О: Количество векторов в векторном пространстве равно кардинальности (или количеству векторов) его базисного набора.
В: Сколько измерений используется для измерения положения?
О: Для измерения положения используются три измерения (длина, ширина и высота). В некоторых случаях может использоваться четвертое (4D) измерение - время - для того, чтобы показать положение события во времени и пространстве.
В: Что означает dim(V)?
О: Dim(V) означает размерность V, которая равна кардинальности (или количеству векторов) его базисного набора или равна количеству направлений прямых линий, которые он имеет.
В: Существует ли одно определение, которое удовлетворяет всем понятиям, связанным с размерностью?
О: Нет, не существует единого определения, которое могло бы удовлетворить все понятия, связанные с размерами.
искать