Экспонента
В математике экспоненциальная функция - это функция, которая быстро растет. Точнее, это функция exp ( x ) = e x {\displaystyle \exp(x)=e^{x}} 
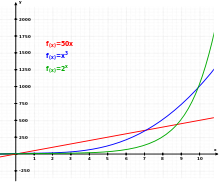
Три различные функции: Линейная (красная), Кубическая (синяя) и Экспоненциальная (зеленая).
Свойства
Поскольку экспоненциальные функции используют экспоненцию, они подчиняются тем же правилам. Таким образом,
exp ( x + y ) = exp ( x ) exp ( y ) = e x + y {\displaystyle \exp(x+y)=\exp(x)\exp(y)=e^{x+y}} 

Натуральный логарифм - это обратная операция экспоненциальной функции.
ln ( x ) = log e ( x ) = log ( x ) log ( e ) {\displaystyle \ln(x)=\log _{e}(x)={\frac {\log(x)}{\log(e)}}}}
Экспоненциальная функция удовлетворяет интересному и важному свойству в дифференциальном исчислении,
d d x e x = e x {\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}e^{x}=e^{x}} 
Это означает, что наклон экспоненциальной функции равен самой экспоненциальной функции, и впоследствии это означает, что она имеет наклон 1 при x = {\displaystyle0 x=0}
Приложения
Экспоненциальная функция является одной из самых полезных математических функций. Она используется для представления экспоненциального роста, который применяется практически во всех научных дисциплинах, а также широко распространен в финансах. Экспоненциальный распад также имеет место, например, радиоактивный распад и поглощение света.
Одним из примеров экспоненциальной функции в реальной жизни являются проценты в банке. Если человек кладет 100 фунтов стерлингов на счет, который получает 3% процентов в месяц, то баланс каждый месяц будет таким (при условии, что деньги не тронуты):
| Месяц | Баланс | Месяц | Баланс |
| Январь | £100.00 | Июль | £119.41 |
| Февраль | £103.00 | Август | £122.99 |
| Март | £106.09 | Сентябрь | £126.68 |
| Апрель | £109.27 | Октябрь | £130.48 |
| Май | £112.55 | Ноябрь | £134.39 |
| Июнь | £115.93 | Декабрь | £138.42 |
Обратите внимание, как с каждым месяцем увеличиваются дополнительные деньги от процентов. Чем больше первоначальный баланс, тем больше процентов получит человек.
Ниже приведены два математических примера экспоненциальных функций.
| a=2
| a=3
|
Связь с математической константой e
Хотя основанием ( a {\displaystyle a}
Число e важно для каждой экспоненциальной функции. Например, банк выплачивает проценты в размере 0,01 процента каждый день. Один человек берет деньги под проценты и кладет их в коробку. Через 10 000 дней (около 30 лет) у него становится в 2 раза больше денег, чем было в начале. Другой человек берет свои деньги под проценты и кладет их обратно в банк. Поскольку банк теперь платит ему проценты на его проценты, количество денег является экспоненциальной функцией. Через 10 000 дней у него будет не в 2 раза больше денег, чем в начале, а в 2,718145 раз больше, чем в начале. Это число очень близко к числу e. Если банк выплачивает проценты чаще, так что сумма, выплачиваемая каждый раз, меньше, то число будет ближе к числу e.
Человек также может посмотреть на рисунок, чтобы понять, почему число e важно для экспоненциальных функций. На рисунке изображены три разные кривые. Кривая с черными точками - это экспоненциальная функция с основанием немного меньше e. Кривая с короткими черными линиями - это экспоненциальная функция с основанием немного больше e. Синяя кривая - это экспоненциальная функция с основанием, точно равным e. Красная линия - это касательная к синей кривой. Она касается синей кривой в одной точке, не пересекая ее. Человек может видеть, что красная кривая пересекает ось x, линию, идущую слева направо, в точке -1. Это верно только для синей кривой. Именно по этой причине экспоненциальная функция с основанием e является особенной.
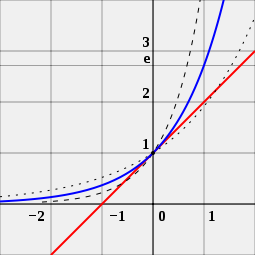
e - это единственное число a, такое, что значение производной экспоненциальной функции f (x) = ax (синяя кривая) в точке x = 0 равно ровно 1. Для сравнения показаны функции 2x (пунктирная кривая) и 4x (пунктирная кривая); они не являются касательными к линии с наклоном 1 (красная).
Вопросы и ответы
В: Что такое экспоненциальная функция?
О: Экспоненциальная функция - это математическая функция, которая растет все быстрее и быстрее.
В: Как математически выражается экспоненциальная функция?
О: Математически экспоненциальная функция выражается как exp(x) = e^x, где e - постоянная Эйлера.
В: Что представляет собой постоянная Эйлера?
О: Константа Эйлера представляет собой иррациональное число, которое приблизительно равно 2,71828.
В: Всегда ли экспоненциальная функция возрастает?
О: Да, экспоненциальная функция всегда увеличивается с ростом x.
В: Есть ли предел тому, как быстро может расти экспоненциальная функция?
О: Нет, нет предела тому, как быстро может расти экспоненциальная функция, поскольку она продолжает расти при больших значениях x.
В: Как мы можем вычислить постоянную Эйлера?
О: Мы можем вычислить постоянную Эйлера с помощью численных методов, таких как ряд Тейлора или продолженные дроби.
В: Какое еще применение имеет экспоненциальная функция, кроме математики?
О: Экспоненциальная функция имеет множество применений за пределами математики, включая физику, химию, биологию, экономику и инженерное дело.
искать

