Теорема о четырёх красках

Точная формулировка проблемы

Интуитивно теорема четырех цветов может быть заявлена как "учитывая любое разделение плоскости на сопредельные области, называемые картой, области могут быть окрашены с использованием максимум четырех цветов, так что никакие две области, которые находятся рядом, не имеют одинаковый цвет". Чтобы правильно решить проблему, необходимо уточнить некоторые аспекты: Во-первых, все точки, которые принадлежат трем или более странам, должны быть проигнорированы. Во-вторых, причудливые карты с регионами конечной области и бесконечным периметром могут потребовать более четырех цветов.

Для целей теоремы каждая "страна" должна быть просто связанным или сопредельным регионом. В реальном мире это не так: Аляска как часть США, Нахчыван как часть Азербайджана и Калининград как часть России не сопредельны. Поскольку территория той или иной страны должна быть одного цвета, четырех цветов может быть недостаточно. Например, рассмотрим упрощенную карту, такую, как та, что показана слева: На этой карте два региона с обозначением А принадлежат одной стране и должны быть одного цвета. Тогда для этой карты требуется пять цветов, так как два региона с обозначением A вместе смешиваются с четырьмя другими регионами, каждый из которых смешивается со всеми остальными. Если А имеет только три области, то может потребоваться шесть или более цветов. Таким образом, можно сделать карты, для которых требуется произвольно большое количество цветов. Аналогичная конструкция также применяется, если для всех водоемов используется один цвет, как это обычно бывает на реальных картах.

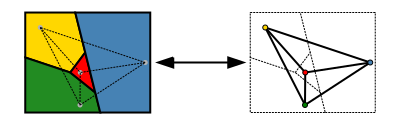
Более легкая в изложении версия теоремы использует теорию графов. Набор областей карты можно представить более абстрактно, как неориентированный граф, имеющий вершину для каждой области и ребро для каждой пары областей, разделяющих граничный отрезок. Этот граф является плоским: он может быть построен на плоскости без пересечений, размещая каждую вершину в произвольно выбранном месте внутри области, которой она соответствует, и рисуя рёбра в виде кривых, которые ведут без пересечений внутри каждой области от места расположения вершины к каждой общей граничной точке области. И наоборот, любой плоскостной график может быть сформирован из карты таким образом. В граф-теоретической терминологии теорема четырех цветов утверждает, что вершины каждого плоского графа могут быть окрашены не более чем в четыре цвета, так что никакие две соседние вершины не будут иметь одинаковый цвет, или, если говорить кратко, "каждый плоский граф четырехцветный" (Thomas 1998, p. 849; Wilson 2002).

Пример карты Азербайджана с неприлежащими регионами


Эта карта не может быть окрашена в четыре цвета

История

Первым, кто назвал эту проблему, был Фрэнсис Гатри, в 1852 году. В то время он был студентом юридического факультета в Англии. Он обнаружил, что ему нужно по крайней мере четыре цвета, чтобы раскрасить карту графств Англии. Август де Морган впервые обсудил проблему в письме, которое он написал Роуэну Хэмлитону в августе 1852 года. В письме де Морган спрашивает, действительно ли четырех цветов достаточно для раскраски карты, чтобы страны, которые находятся рядом друг с другом, получили разные цвета.

Английский математик Артур Кейли представил эту проблему математическому обществу в Лондоне в 1878 году. В течение года Альфред Кемп нашел то, что выглядело как доказательство проблемы. Одиннадцать лет спустя, в 1890 году, Перси Хивуд показал, что доказательства Альфреда ошибочны. Питер Гатри Тейт представил еще одну попытку доказательства в 1880 году. Потребовалось одиннадцать лет, чтобы показать, что доказательство Тейта тоже не сработало. В 1891 году Джулиус Петерсен смог показать это. Когда он сфальсифицировал доказательство Кейли, Кемп также показал доказательство для проблемы, которую он назвал Теоремой пяти цветов. Теорема гласит, что любая такая карта может быть окрашена не более чем в пять цветов. Есть два ограничения: во-первых, любая страна сопредельная, нет никаких эксклавов. Второе ограничение состоит в том, что страны должны иметь общую границу; если они касаются только одной точки, они могут быть окрашены в один и тот же цвет. Несмотря на то, что доказательство Кемпе было неверным, он использовал некоторые идеи, которые впоследствии позволили бы получить правильное доказательство.

В 1960-е и 1970-е годы Генрих Хеш разработал первый эскиз доказательства с помощью компьютера. Кеннет Аппель и Вольфганг Хейкен улучшили этот эскиз в 1976 году (Robertson и др. 1996). Они смогли уменьшить количество случаев, которые должны быть протестированы до 1936 года; более поздняя версия была сделана, которая полагалась на тестирование только 1476 случаев. Каждый случай должен был быть протестирован на компьютере (Appel & Haken 1977).

В 1996 году Нил Робертсон, Дэниел Сандерс, Пол Сеймур и Робин Томас усовершенствовали этот метод и сократили число подлежащих тестированию случаев до 663. Опять же, каждый случай должен был быть протестирован на компьютере.

В 2005 году Жорж Гонтье и Бенджамин Вернер разработали официальное доказательство. Это было улучшением, потому что это позволило впервые использовать программное обеспечение, подтверждающее теоремы. Используемое программное обеспечение называется Coq.

Теорема четырех цветов - это первая большая математическая задача, которая была доказана с помощью компьютера. Поскольку доказательство не может быть сделано человеком, некоторые математики не признали его правильным. Для проверки доказательства необходимо полагаться на правильно работающее программное и аппаратное обеспечение. Поскольку доказательство было сделано компьютером, оно также не очень элегантно.

Попытки, которые оказались неправильными

Теорема четырех цветов за свою долгую историю привлекла большое количество ложных доказательств и опровержений. Сначала "Нью-Йорк Таймс" отказалась сообщить о доказательствах Аппель-Хейкена. Газета сделала это в рамках своей политики; она опасалась, что доказательства будут показаны ложными, как и те, что были до нее (Wilson 2002, p. 209). На некоторые доказательства ушло много времени, пока они не могли быть сфальсифицированы: Для того, чтобы доказательства Кемпе и Таита сфальсифицировали их, потребовалось более десяти лет.

Самые простые контрпримеры, как правило, пытаются создать одну область, которая касается всех остальных. Это заставляет остальные регионы окрашиваться только в три цвета. Поскольку теорема четырех цветов верна, это всегда возможно, однако, поскольку человек, рисующий карту, фокусируется на одном большом регионе, он не замечает, что остальные регионы на самом деле могут быть окрашены в три цвета.

Этот трюк можно обобщить: Если заранее выбрать цвета некоторых регионов на карте, становится невозможным окрасить оставшиеся регионы таким образом, что в общей сложности используются только четыре цвета. Кто-то, проверяющий контрпример, может не подумать, что может понадобиться изменить цвет этих регионов. В результате контрпример будет выглядеть корректно, даже если это не так.

Возможно, одним из эффектов, лежащих в основе этого распространенного заблуждения, является то, что ограничение цвета не является переходным: регион только должен быть окрашен в цвет, отличный от регионов, к которым он непосредственно прикасается, а не от регионов, к которым он прикасается. Если бы это было ограничение, плоскостные графики потребовали бы произвольно большого количества цветов.

Другие ложные опровержения нарушают предположения теоремы неожиданными способами, например, использование области, имеющей несколько разъединенных частей, или не допускающей касания в точке областей одного и того же цвета.

Раскрашивание политических карт

В реальной жизни во многих странах есть эксклавы или колонии. Поскольку они принадлежат стране, они должны быть окрашены в тот же цвет, что и родительская страна. Это означает, что обычно для окраски такой карты требуется более четырех цветов. Когда математики говорят о графе, связанном с проблемой, они говорят, что он не плоский. Несмотря на то, что легко проверить, является ли граф плоским, найти наименьшее количество цветов, необходимых для окраски, очень сложно. Это NP-завершенность, которая является одной из самых сложных проблем, которые существуют. Наименьшее количество цветов, необходимое для окраски графа, известно как его хроматическое число. Многие из задач, которые возникают при попытке решить теорему четырех цветов, связаны с дискретной математикой. По этой причине часто используются методы из алгебраической топологии.

Расширение на "не плоские" карты

Теорема четырех цветов требует, чтобы "карта" находилась на плоской поверхности, которую математики называют плоскостью. В 1890 году Перси Джон Хьювуд создал то, что сегодня называется догадкой Хьювуда: Она задает тот же вопрос, что и теорема о четырех цветах, но для любого топологического объекта. В качестве примера можно привести торус, окрашенный не более чем в семь цветов. Предположение Heawood дает формулу, которая работает для всех таких объектов, кроме бутылки Кляйна.