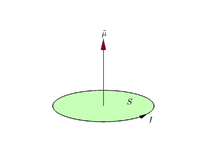
Магнитный момент

Два определения момента

В учебниках для определения магнитных моментов используются два взаимодополняющих подхода. В учебниках до 1930-х годов они определялись с помощью магнитных полюсов. В большинстве современных учебников они определяются в терминах амперовских токов.

Определение магнитного полюса

Физики представляют источники магнитных моментов в материалах в виде полюсов. Северный и южный полюса являются аналогией положительных и отрицательных зарядов в электростатике. Рассмотрим стержневой магнит, который имеет магнитные полюса одинаковой величины, но противоположной полярности. Каждый полюс является источником магнитной силы, которая ослабевает с расстоянием. Поскольку магнитные полюса всегда располагаются парами, их силы частично аннулируют друг друга, поскольку в то время как один полюс притягивается, другой отталкивается. Эта аннулирующая сила больше всего проявляется, когда полюса находятся близко друг к другу, т.е. когда магнит короткий. Поэтому магнитная сила, создаваемая магнитом в данной точке пространства, зависит от двух факторов: от силы p {\displaystyle p} его полюсов и от вектора l {\displaystyle \mathbf {l} }, разделяющем их. Момент определяется как

m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . }

Он направлен в направлении от южного полюса к северному. Аналогию с электрическими диполями не следует принимать слишком далеко, поскольку магнитные диполи связаны с угловым моментом (см. Магнитный момент и угловой момент). Тем не менее, магнитные полюса очень полезны для магнитостатических расчетов, особенно в приложениях к ферромагнетикам. Практики, использующие подход с магнитными полюсами, обычно представляют магнитное поле ирротационным полем H {\displaystyle \mathbf {H} } , по аналогии с электрическим полем E {\displaystyle \mathbf {E} } .

Определение токовой петли

Предположим, что в плоском замкнутом контуре протекает электрический ток I {\displaystyle I} и площадь вектора S {\displaystyle \mathbf {S} } ( x {\displaystyle x} , y {\displaystyle y} , и z {\displaystyle z} координаты этого вектора являются областями проекций контура на y z {\displaystyle yz} , z x {\displaystyle zx} , и x y {\displaystyle xy} плоскости). Его магнитный момент m {\displaystyle \mathbf {m} } , вектор, определяется как:

m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . }

По условию, направление векторной области задается правилом захвата правой рукой (скручивание пальцев правой руки в направлении тока вокруг петли, когда ладонь руки "касается" внешнего края петли, а прямой большой палец указывает направление векторной области и, следовательно, магнитного момента).

Если петля не плоская, то момент приводится к виду

m = I ∫2 r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . }

В самом общем случае произвольного распределения тока в пространстве магнитный момент такого распределения можно найти из следующего уравнения:

m = ∫12 r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,}

где r {\displaystyle \mathbf {r} } - вектор положения, направленный от начала координат к месту расположения элемента объема, а J {\displaystyle \mathbf {J} } - вектор плотности тока в этом месте.

Приведенное выше уравнение может быть использовано для расчета магнитного момента любой совокупности движущихся зарядов, например, вращающегося заряженного твердого тела, путем подстановки

J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,}

где ρ {\displaystyle \rho } - плотность электрического заряда в данной точке, а v {\displaystyle \mathbf {v} } - мгновенная линейная скорость этой точки.

Например, магнитный момент, создаваемый электрическим зарядом, движущимся по круговой траектории, равен

m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } ,

где r {\displaystyle \mathbf {r} } - положение заряда q {\displaystyle q} относительно центра круга, а v {\displaystyle \mathbf {v} } - мгновенная скорость заряда.

Практики, использующие модель токовой петли, обычно представляют магнитное поле соленоидальным полем B {\displaystyle \mathbf {B} } , аналогично электростатическому полю D {\displaystyle \mathbf {D} } .

Магнитный момент соленоида

Обобщением приведенного выше контура тока является многовитковая катушка, или соленоид. Его момент является векторной суммой моментов отдельных витков. Если соленоид имеет N {\displaystyle N} одинаковых витков (однослойная обмотка),

m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . }

Трехмерное изображение соленоида.


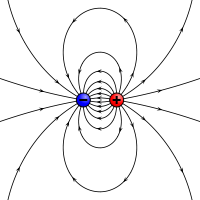
Электростатический аналог магнитного момента: два противоположных заряда, разделенных конечным расстоянием.

Единицы

Единица измерения магнитного момента не является базовой единицей в Международной системе единиц (СИ) и может быть представлена более чем одним способом. Например, в определении токовой петли площадь измеряется в квадратных метрах, а I {\displaystyle I} измеряется в амперах, поэтому магнитный момент измеряется в ампер-квадратных метрах ( A m {\displaystyle2 {\text{A m}}^{2}}). В уравнении для крутящего момента момент измеряется в Ньютон.метрах, а магнитное поле в теслах, поэтому момент измеряется в Н.м на Тесла ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}}). Эти два представления эквивалентны:

A m =2 N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. }

В системе CGS существует несколько различных наборов единиц измерения электромагнетизма, основными из которых являются ESU, Gaussian и EMU. Среди них есть две альтернативные (неэквивалентные) единицы магнитного дипольного момента в CGS:

(ESU CGS) 1 статА-см² = 3,33564095×10^-14 (м-А² или Н.м/Т)

и (более часто используемые)

(EMU CGS и Gaussian-CGS) 1 эрг/Г = 1 абА-см² = 10^-3 (м-А² или Н.м/Т).

Отношение этих двух неэквивалентных единиц КГС (EMU/ESU) в точности равно скорости света в свободном пространстве, выраженной в см/с.

Все формулы в этой статье верны в единицах СИ, но в других системах единиц формулы, возможно, придется изменить. Например, в единицах СИ контур тока с током I и площадью A имеет магнитный момент I×A (см. ниже), но в гауссовых единицах магнитный момент равен I×A/c.

Внутренние магнитные моменты и спины некоторых элементарных частиц
Частица	Магнитный дипольный момент в единицах СИ (10 −27Дж/Т)	Спиновое квантовое число (безразмерное)
электрон	-9284.764	1/2
протон	14.106067	1/2
нейтрон	-9.66236	1/2
мюон	-44.904478	1/2
дейтрон	4.3307346	1
тритон	15.046094	1/2

Связь между понятиями магнитного момента и намагниченности см. в разделе "Намагниченность".