Ускорение под действием силы тяжести

Почему тяжелые предметы падают не быстрее легких

Исаак Ньютон установил, что результирующая сила равна массе, умноженной на ускорение, или, в символах, F = m a {\displaystyle F=ma} . Это можно перефразировать, чтобы получить a = F m {\displaystyle a={\frac {F}{m}}\ }\ } . Чем больше масса падающего объекта, тем больше сила гравитационного притяжения, притягивающая его к Земле. В приведенном выше уравнении это F {\displaystyle F} . Однако количество раз, во сколько сила становится больше или меньше, равно количеству раз, во сколько масса становится больше или меньше, при этом соотношение остается постоянным. В любой ситуации F m {\displaystyle {\frac {F}{m}}\ } аннулируется до равномерного ускорения около 9,8 м/с² . Это означает, что, независимо от массы, все свободно падающие объекты ускоряются с одинаковой скоростью.

Рассмотрим следующие примеры:

a = 49 Н 5 k g = 9,8 Н / k g = 9,8 м / с 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }

a = 147 Н 15 к g = 9,8 Н / к g = 9,8 м / с 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }

Ускорение поверхности

В зависимости от местоположения, объект на поверхности Земли падает с ускорением от 9,76 до 9,83 м/с² (32,0 - 32,3 фута/с² ).

Земля не совсем сферическая. Она похожа на "сжатую" сферу, радиус которой на экваторе немного больше, чем радиус на полюсах. Это приводит к тому, что гравитационное ускорение немного увеличивается на полюсах (поскольку мы находимся близко к центру Земли, а сила гравитации зависит от расстояния) и немного уменьшается на экваторе. Кроме того, из-за центростремительного ускорения ускорение, вызванное гравитацией, немного меньше на экваторе, чем на полюсах. Изменения в плотности породы под землей или наличие гор поблизости могут незначительно повлиять на гравитационное ускорение.

Высота

Ускорение объекта изменяется с высотой. Изменение гравитационного ускорения с расстоянием от центра Земли происходит по закону обратного квадрата. Это означает, что гравитационное ускорение обратно пропорционально квадрату расстояния от центра Земли. При увеличении расстояния в два раза гравитационное ускорение уменьшается в 4 раза, при увеличении расстояния в три раза гравитационное ускорение уменьшается в 9 раз и так далее.

гравитационное ускорение ∝ 1 расстояние 2 {\displaystyle {\mbox{gravitational acceleration}}\ \ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}}\ }

гравитационное ускорение × расстояние 2 = k {\displaystyle {\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}}

На поверхности Земли ускорение, вызванное гравитацией, составляет примерно 9,8 м/с² (32 фута/с² ). Среднее расстояние до центра Земли составляет 6 371 км (3 959 миль).

k = 9,8 × 6371 2 {\displaystyle {k}={\mbox{9,8}}\ \times {{\mbox{6371}}^{2}}}}}

Используя константу k {\displaystyle k} , мы можем вычислить гравитационное ускорение на определенной высоте.

гравитационное ускорение = k расстояние 2 {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}}\ }

Пример: Найдите ускорение, вызванное силой тяжести на высоте 1000 км (620 миль) над поверхностью Земли.

6371 + 1000 = 7371 {\displaystyle 6371+1000=7371}

∴ Расстояние от центра Земли составляет 7 371 км (4 580 миль).

гравитационное ускорение = 9,8 × 6371 2 7371 2 ≈ 7,3 {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9,8}}\ \times {{\mbox{6371}}^{2}}}}{{\mbox{7371}}^{2}}}\ \approx 7,3}}.

∴ Ускорение под действием силы тяжести на высоте 1000 км (620 миль) над поверхностью Земли составляет 7,3 м/с² (24 фута/с² ).

Гравитационное ускорение на линии Кармана, границе между атмосферой Земли и космическим пространством, которая проходит на высоте 100 км (62 мили), всего на 3% ниже, чем на уровне моря.

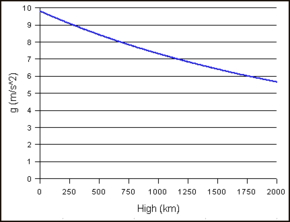
Изменение гравитационного ускорения с высотой объекта