Фрактал

Примеры

Существует множество типов фракталов, выполненных самыми разнообразными способами. Одним из примеров является треугольник Серпинского, в котором внутри большого треугольника находится бесконечное количество маленьких треугольников. Другой пример - множество Мандельброта, названное в честь Бенуа Мандельброта. Треугольник Серпинского строится с помощью узоров, а множество Мандельброта основано на уравнении.

В природе также существует множество естественных примеров фракталов, включая деревья, снежинки, некоторые овощи и береговые линии.

Кривая Коха

Кривая Коха - простой пример фрактала. Для начала возьмите часть прямой линии - так называемый отрезок прямой. Разрежьте линию на 3 одинаковые по размеру части. Избавьтесь от середины этих кусков и вставьте в них верхнюю часть треугольника со сторонами той же длины, что и вырезанный кусок. Теперь у нас есть 4 отрезка линии, которые соприкасаются на концах. Теперь мы можем сделать то же самое, что и с первым отрезком, с каждым из 4 кусочков. Теперь мы можем проделать то же самое снова и снова со всеми битами, которые у нас получились. Теперь мы будем делать это бесконечно и посмотрим, что получится в итоге.

Длина кривой Коха равна бесконечности, а площадь кривой Коха равна нулю. Это довольно странно. Отрезок прямой (с размерностью 1) может иметь длину 1, но его площадь равна 0. Квадрат длиной 1 и шириной 1 (с размерностью 2) будет иметь площадь 1 и длину бесконечность.

Измерение сходства

Так, кривая Коха кажется больше, чем что-то с размерностью 1, и меньше, чем что-то с размерностью 2. Идея размерности подобия заключается в том, чтобы дать размерность, которая дает лучшее представление о длине или площади фракталов. Таким образом, для кривой Коха мы хотим получить размерность между 1 и 2.

Кривая Коха может быть разрезана на четыре части, каждая из которых составляет 1 3 {\displaystyle {\frac {1}{3}}}} от размера оригинала. Мы называем количество частей, на которые можно разрезать фрактал, N {\displaystyle N} , а разность размеров B {\displaystyle B} . Подставим их в уравнение:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}}}}}

Где log {\displaystyle \log } - логарифм числа. Это число - размерность Хаусдорфа фрактала. В кривой Коха это log 4 - log 1 3 = 1.2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619... } как мы и хотели.

Кривая Коха - одна из самых простых фрактальных фигур, поэтому ее размерность легко определить. Ее размерность подобия и размерность Хаусдорфа одинаковы. Для более сложных фракталов это не так.

Снежинка Коха

Снежинка Коха (или звезда Коха) - это то же самое, что и кривая Коха, только начинается она не с отрезка прямой, а с равностороннего треугольника.

Как сделать кривую Коха

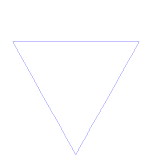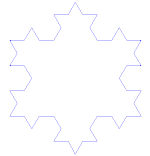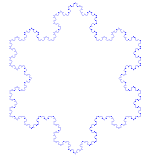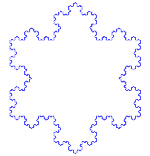
Использует

Фракталы имеют множество применений, например, в биологии (легкие, почки, вариабельность сердечного ритма и т.д...), в землетрясениях, в финансах, где они связаны с так называемыми распределениями с тяжелыми хвостами, и в физике. Это говорит о том, что фракталы необходимо изучать, чтобы понять, почему фракталы так часто встречаются в природе.

Некоторые фракталы существуют только по художественным причинам, но другие очень полезны. Фракталы являются очень эффективными формами для радиоантенн и используются в компьютерных чипах для эффективного соединения всех компонентов. Кроме того, береговые линии можно рассматривать как фракталы.