элементарная алгебра
Элементарная алгебра - это самая базовая форма алгебры, которой учат студентов. Часто она является одной из следующих областей математики, преподаваемых ученикам после арифметики. Если в арифметике встречаются только числа и операторы типа +, -, × и ÷, то в алгебре под числами понимаются переменные (например, a, x, y). Это полезно, потому что:
- Это позволяет людям решать проблемы с "неизвестными" числами. Это означает изучение уравнений и способов их решения (например, "найти число x, где 3 x + 1 = 10 {\displaystyle 3x+1=10}
").
- Это позволяет обобщать правила из арифметики. В то время как некоторые ученики понимают, что 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3}
Это помогает доказать, что a + b = b + a {\displaystyle a+b=b+a}
для всех a и b. Это делает алгебру хорошим шагом к изучению абстракции (изучение общих идей из многих примеров).
- Она помогает людям понять и создать функциональные взаимосвязи (также иногда называемые причиной и следствием). Пример этого: "если x билетов будет продано, то прибыль составит 3 x - 10 {\displaystyle 3x-10}
долларов".
Эти три основные нити элементарной алгебры. Элементарная алгебра часто используется во многих других предметах, таких как наука, бизнес и строительство. Абстрактная алгебра, гораздо более продвинутая тема, как правило, преподается в конце колледжа.
Простые проблемы с алгеброй
Если уравнение имеет только одно неизвестное число, то иногда его легко решить. Неизвестное число называется "x":
2 x + 4 = 12. {\displaystyle 2x+4=12.,}
Для решения простого уравнения с одной неизвестной суммой прибавить, вычесть, умножить или разделить обе стороны уравнения на одно и то же число, чтобы поставить неизвестную сумму, х, на одну сторону уравнения. После того, как х сам по себе окажется с одной стороны, используйте арифметику для определения суммы с другой стороны уравнения. Например, вычитая 4 с обеих сторон уравнения выше:
2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4,}
Получаю:
2 x = 8 {\displaystyle 2x=8,}
Делим обе стороны на 2:
2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2},}
Получаю:
x = 4. {\displaystyle x=4.,}
Это может помочь думать об этом уравнении как о пиле или балансе, что вы делаете с одной стороны, что вы должны делать с другой, и ваша главная цель - получить x сам по себе.
Определения
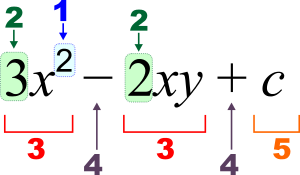
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c}
1: Экспонента (мощность), 2: Коэффициент, 3: член, 4: оператор, 5: константа, x, y {\displaystyle x,y} : 
Вопросы и ответы
В: Что такое элементарная алгебра?
О: Элементарная алгебра - это самая базовая форма алгебры, которую преподают студентам. Она обычно следует за арифметикой и включает использование переменных (таких как a, x, y) для обозначения чисел в уравнениях.
В: Каковы некоторые области применения элементарной алгебры?
О: Элементарная алгебра может использоваться для решения задач о неизвестных числах, обобщения правил из арифметики, понимания и создания функциональных зависимостей, а также часто используется во многих других предметах, таких как наука, бизнес и строительство.
В: Как элементарная алгебра помогает людям понять абстрактные идеи?
О: Элементарная алгебра помогает людям усвоить общие идеи на множестве примеров, доказывая, что a+b=b+a для всех a и b. Это позволяет им лучше понять абстрактные понятия.
В: Является ли абстрактная алгебра более продвинутой, чем элементарная алгебра?
О: Да, абстрактная алгебра обычно преподается в колледже на поздних курсах и является более продвинутой, чем элементарная алгебра.
В: Какие типы уравнений включает в себя элементарная алгебра?
О: Элементарная алгебра включает в себя уравнения с переменными (например, a, x, y), обозначающими числа, а также операторы +,-,×,и ÷.
3x+1=10 {\displaystyle 3x+1=10}
В: Как понимание элементарной алгебры может помочь в изучении других предметов?
О: Понимание элементарной алгебры может помочь в изучении других предметов, таких как наука, бизнес или строительство, поскольку она позволяет решать задачи о неизвестных числах и создавать функциональные зависимости между различными переменными.
искать




