Алгебра

История

Ранние формы алгебры были разработаны вавилонянами и греческими геометрами, такими как Герой Александрии. Однако слово алгебра - это латинская форма арабского слова ал-джабр ("кастинг") и происходит от математического сборника ал-макала фи Хисаб-аль-джабр ва-аль-мукабилах ("очерк о расчете кастинга и уравнения"), написанного в IX в. персидским математиком мухаммадом ибн муса ал-хваризми - мусульманином, родившимся в хурезме в узбекском народе. Он процветал при Аль-Ма'мауре в Багдаде (Ирак) в 813-833 гг. н.э. и умер около 840 г. н.э. Книга была привезена в Европу и переведена на латинский язык в XII веке. Затем книга получила название "Алгебра". (Окончание названия математика, аль-Хорезми, было изменено на слово, которое легче произносится на латинском языке, и стало алгоритмом английского слова).

Примеры

Вот простой пример проблемы алгебры:

У Сью 12 конфет, у Энн 24. Они решили поделиться так, чтобы у них было столько же конфет. Сколько конфет будет у каждой?

Это те шаги, которые вы можете использовать для решения проблемы:

1. Чтобы получить такое же количество конфет, Энн должна отдать их Сью. Пусть х представляет количество конфет, которое Энн отдаст Сью.
2. Конфеты Сью плюс икс должны быть такими же, как конфеты Энн минус икс. Это написано так: 12 + х = 24 - х
3. Вычитайте 12 из обеих сторон уравнения. Это дает: x = 12 - x. (То, что происходит с одной стороны знака равенства, должно произойти и с другой стороны, чтобы уравнение все еще оставалось верным. Таким образом, в этом случае, когда 12 вычитается с обеих сторон, средний шаг 12 + x - 12 = 24 - x - 12. После того, как человеку это удобно, средняя ступень не записывается)).
4. Добавьте x в обе стороны уравнения. Это дает: 2x = 12
5. Разделите обе стороны уравнения на 2, что дает x = 6. Ответ - 6. Если Энн даст 6 конфет, то они будут иметь одинаковое количество конфет.
6. Чтобы проверить это, верните 6 обратно в исходное уравнение, где бы ни был x: 12 + 6 = 24 - 6.
7. Это дает 18=18, что правда. Теперь у каждого из них по 18 конфет.

На практике алгебра может быть использована, когда сталкиваешься с проблемой, которая слишком сложна для решения каким-либо другим способом. Такие проблемы, как строительство автострады, проектирование мобильного телефона или поиск лекарства от болезни - все они требуют алгебры.

Написание алгебры

Как и в большинстве математических частей, сложение z к y (или y плюс z) пишется как y + z. Вычитание z из y (или y минус z) пишется как y - z. Деление y на z (или y на z: y z {\displaystyle y \over z} ) пишется как y ÷ z или y/z. y/z.

В алгебре умножение y на z (или y на z) может быть записано 4 способами: y × z, y * z, y-z, или просто yz. Символ умножения "×" обычно не используется, так как он слишком похож на букву x, которая часто используется в качестве переменной. Также при умножении более крупного выражения можно использовать круглые скобки: y (z+1).

Когда мы умножаем число и букву в алгебре, мы пишем число перед буквой: 5 × y = 5 гр. Когда число 1, то 1 не пишется, потому что 1 раз любое число является этим числом (1 × y = y) и поэтому оно не нужно.

В качестве примечания не обязательно использовать буквы x или y в алгебре. Переменные - это просто символы, которые означают какое-то неизвестное число или значение, поэтому вы можете использовать любую переменную. x и y - наиболее распространенные переменные.

Функции и графики

Важной частью алгебры является изучение функций, так как функции часто появляются в уравнениях, которые мы пытаемся решить. Функция подобна машине, в которую можно вставить число (или числа) и вывести определенное число (или числа). При использовании функций, графики могут быть мощными инструментами, помогающими нам изучать решения уравнений.

График - это рисунок, на котором показаны все значения переменных, которые делают уравнение или неравенство истинным. Обычно это легко сделать, когда есть только одна или две переменные. Часто график представляет собой линию, и если линия не изгибается и не идет прямо вверх-вниз, то ее можно описать по базовой формуле y = mx + b. Переменная b - это y-вход графа (где линия пересекает вертикальную ось), а m - наклон или крутизна линии. Эта формула применяется к координатам графа, где записана каждая точка линии (x, y).

В некоторых математических задачах, например, в уравнении для строки, может быть более одной переменной (в данном случае x и y). Для нахождения точек на прямой изменяется одна переменная. Изменяемая переменная называется "независимой". Затем производится подсчет числа. Сделанное число называется "зависимой" переменной. Большую часть времени независимая переменная записывается как x, а зависимая - как y, например, в y = 3x + 1. Часто это записывается на графе по осям x (идущим влево и вправо) и y (идущим вверх и вниз). Она также может быть записана в виде функции: f(x) = 3x + 1. Таким образом, в данном примере мы можем поставить 5 для x и получить y = 16. Если вставить 2 для x, то получится y=7. А 0 для x получится y=1. Так получилась бы прямая, проходящая через точки (5,16), (2,7) и (0,1), как видно на графике справа.

Если х имеет мощность 1, то это прямая линия. Если она в квадрате или другой силе, то она будет изогнута. Если она использует неравенство (< или > ), то обычно часть графика заштриховывается, либо выше, либо ниже линии.

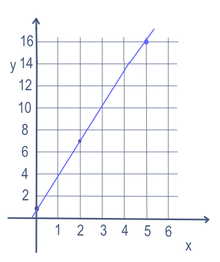
Линейное уравнение для y=3x+1

Правила алгебры

В алгебре есть несколько правил, которые могут быть использованы для дальнейшего понимания уравнений. Они называются правилами алгебры. Хотя эти правила могут показаться бессмысленными или очевидными, разумно понимать, что эти свойства присущи не всем ветвям математики. Поэтому будет полезно узнать, как декларируются эти аксиоматические правила, прежде чем принимать их как должное. Прежде чем перейти к правилам, поразмышляйте над двумя определениями, которые будут даны.

1. Напротив - противоположность {\displaystyle -a} является - a {\displaystyle -a} .
2. Взаимодействие - ответная величина {\displaystyle a} равна 1 a {\displaystyle {\frac {1}{a}}} .

Правила

Коммутативное свойство дополнения

Комментарий" означает, что функция имеет тот же результат, если происходит замена чисел. Другими словами, порядок слагаемых в уравнении не имеет значения. Когда оператором двух членов является сложение, применяется "коммутативное свойство сложения". В алгебраических терминах это дает a + b = b + a {\displaystyle a+b=b+a} .

Обратите внимание, что это не относится к вычитанию! (т.е. a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Коммутативное свойство умножения

Когда оператором двух членов является умножение, применяется "коммутативное свойство умножения". В алгебраических терминах это дает ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Обратите внимание, что это не относится к делению! (т.е. a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}} когда ≠ b {\displaystyle a\neq b} )

Добавочное имущество

Под "ассоциативным" понимается группировка чисел. Ассоциативное свойство сложения подразумевает, что при сложении трех и более терминов не имеет значения, как эти термины сгруппированы. Алгебраически это дает a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Обратите внимание, что это не означает вычитания, например, 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (см. свойство дистрибутива).

Ассоциированное свойство умножения

Ассоциативное свойство умножения подразумевает, что при умножении трех и более терминов не имеет значения, как эти термины сгруппированы. Алгебраически это дает ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Обратите внимание, что это не означает деления, например, 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Дистрибьюторская собственность

Распределительное свойство гласит, что можно распределить умножение числа на другой член. Например: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Не путайте это с ассоциативными свойствами! Например: a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .) .) .

Добавочное свойство личности

Под "Идентификацией" понимается свойство числа, равное самому себе. Другими словами, существует операция, состоящая из двух чисел, так что она равна переменной суммы. Аддитивное свойство "Идентичность" указывает, что сумма любого числа и 0 является этим числом: a + 0 = a {\displaystyle a + 0=a} . Это также означает вычитание: a - 0 = a {\displaystyle a-0=a} .

Мультипликативная идентификация собственности

В свойстве мультипликативной идентификации указано, что произведение любого числа и 1 является этим числом: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . Это также означает деление: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Обратное свойство добавки

Обратное свойство добавки несколько противоположно свойству идентификации добавки. Когда операция является суммой числа и его противоположностью, и она равна 0, то эта операция является действительной алгебраической операцией. Алгебраически она гласит: a - a = 0 {\displaystyle a-a=0} . Добавочный инверс 1 равен (-1).

Мультипликативная обратная собственность

Мультипликативное обратное свойство подразумевает, что когда операция является произведением числа и его обратной величины, а она равна 1, то эта операция является действительной алгебраической операцией. Алгебраически оно гласит: a = 1 {\displaystyle {\frac {a}{a}}=1} . Мультипликативный инверс 2 равен 1/2.

Расширенная алгебра

Помимо "элементарной алгебры", или базовой алгебры, существуют продвинутые формы алгебры, преподаваемые в колледжах и университетах, такие как абстрактная алгебра, линейная алгебра и универсальная алгебра. Сюда входит и то, как использовать матрицу для решения многих линейных уравнений одновременно. Абстрактная алгебра - это изучение вещей, которые встречаются в уравнениях, переходя от чисел к более абстрактным с группами чисел.

Многие математические проблемы связаны с физикой и инженерией. Во многих из этих проблем физики время является переменной. Время использует букву t. Использование основных идей алгебры может помочь свести математическую задачу к ее простейшей форме, облегчая решение сложных задач. Энергия - это e, сила - это f, масса - это m, ускорение - это a и скорость света - иногда c. Это используется в некоторых известных уравнениях, таких как f = ma и e =mc^2 (хотя для придумывания последнего уравнения потребовалась более сложная математика, выходящая за рамки алгебры).

Связанные страницы

• Список тем по математике
• Порядок операций
• Парабола
• Компьютерная алгебра