преобразование Фурье
Преобразование Фурье - это математическая функция, которая может быть использована для поиска базовых частот, составляющих сигнал или волну. Например, если играет аккорд, звуковая волна аккорда может быть подана на преобразование Фурье, чтобы найти ноты, из которых сделан аккорд. Выходное преобразование Фурье иногда называют частотным спектром или распределением, так как оно отображает спектр частот входного сигнала. Эта функция имеет много применений в криптографии, океанографии, машинном обучении, радиологии, квантовой физике, а также в звуковом проектировании и визуализации.
Фурье-преобразование функции f ( x ) {\displaystyle f(x)}
дается с помощью функции
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx} 
α {\displaystyle \alpha }
это частота
F ( α ) {\displaystyle F(\alpha )}
является функцией преобразования Фурье и возвращает значение, представляющее собой преобладающую частоту α {\displaystyle \alpha } в исходном сигнале.
e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} 
Представляет собой обертку входной функции f ( x ) {\displaystyle f(x)} вокруг начала в комплексной плоскости на некоторой частоте α {\displaystyle \alpha }.
Обратное преобразование Фурье дается посредством
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha } 
Преобразование Фурье показывает, какие частоты находятся в сигнале. Например, рассмотрим звуковую волну, которая содержит три различные музыкальные ноты: A, B и C. Составляя график преобразования Фурье этой звуковой волны (с частотой по оси x и интенсивностью по оси y), вы увидите пик на каждой частоте, который соответствует одной из музыкальных нот.
Многие сигналы могут быть созданы путем сложения косинусов и синусоидальных сигналов с различными амплитудами и частотами. Фурье преобразовывает графики амплитуд и фаз этих косинусов и синусов против их соответствующих частот.
Трансформации Фурье важны, потому что многие сигналы имеют больший смысл, когда их частоты разделены. В аудио примере выше, глядя на сигнал по отношению к времени не делает очевидным, что ноты A, B, и C находятся в сигнале. Многие системы делают разные вещи на разных частотах, поэтому такие системы могут быть описаны тем, что они делают с каждой частотой. Примером этого является фильтр, который блокирует высокие частоты.
Вычисление преобразования Фурье требует понимания интеграции и мнимых чисел. Компьютеры обычно используются для вычисления преобразования Фурье из чего угодно, но не из простейших сигналов. Быстрое преобразование Фурье - это метод, используемый компьютерами для быстрого вычисления преобразования Фурье.
· 
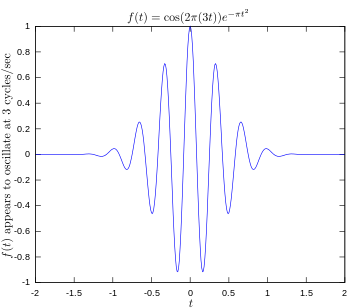
Оригинальная функция, показывающая колебание сигнала на частоте 3 герц.
· 
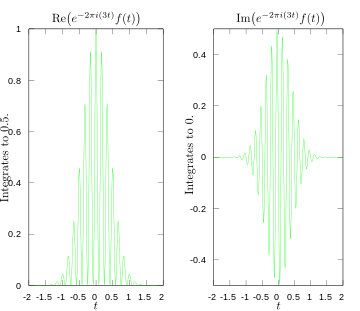
Реальная и воображаемая части подынтегральной части для преобразования Фурье на частоте 3 герц
· 
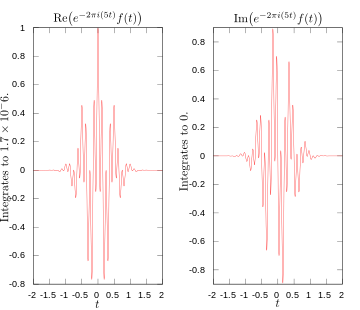
Реальная и воображаемая части подынтегральной части для преобразования Фурье на частоте 5 герц
· 
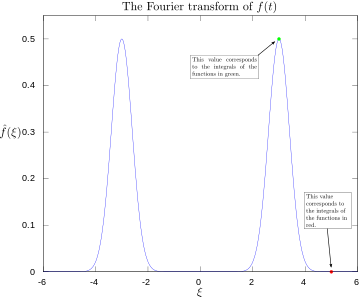
Фурье-преобразование с 3 и 5 герц маркировкой.
Вопросы и ответы
В: Что такое преобразование Фурье?
О: Преобразование Фурье - это математическая функция, которая может быть использована для нахождения базовых частот, из которых состоит волна. Оно берет сложную волну и находит частоты, из которых она состоит, что позволяет определить ноты, составляющие аккорд.
В: Каковы некоторые области применения преобразования Фурье?
О: Преобразование Фурье находит широкое применение в криптографии, океанографии, машинном обучении, радиологии, квантовой физике, а также в звуковом дизайне и визуализации.
В: Как рассчитывается преобразование Фурье?
О: Преобразование Фурье функции f(x) определяется как F(ב) = ∫-∞+∞f(x)e-2נiבxdx, где ב - частота. Это возвращает значение, представляющее, насколько частота ב преобладает в исходном сигнале. Обратное преобразование Фурье имеет вид f(x) = ∫-∞+∞F(ב)e+2נixבdב.
В: Как выглядит выходной сигнал преобразования Фурье?
О: Выходной сигнал преобразования Фурье можно назвать либо частотным спектром, либо распределением, поскольку он отображает распределение возможных частот входного сигнала.
В: Как компьютеры вычисляют быстрое преобразование Фурье?
О: Компьютеры используют алгоритм под названием Быстрое преобразование Фурье (БПФ) для быстрого вычисления любых, кроме самых простых, преобразований сигналов.
В: Что нам не показывает рассмотрение сигналов в зависимости от времени?
О: Рассмотрение сигналов относительно времени не позволяет понять, какие ноты в них присутствуют; многие сигналы становятся более понятными, когда их частоты разделяются и анализируются по отдельности.
