Точечное произведение

В математике точечное произведение - это операция, которая принимает на вход два вектора, а на выходе возвращает скалярное число. Возвращаемое число зависит от длины обоих векторов и от угла между ними. Название происходит от центрированной точки "-", которая часто используется для обозначения этой операции; альтернативное название скалярное произведение подчеркивает скалярную (а не векторную) природу результата.

Точечное произведение контрастирует (в трехмерном пространстве) с перекрестным произведением, в результате которого получается вектор.

Определение

Точечное произведение двух векторов a = [a₁ , a₂ , ..., a_n ] и b = [b₁ , b₂ , ..., b_n ] определяется как:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}} $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

где Σ обозначает обозначение суммирования (сумма всех членов), а n - размерность векторного пространства.

В размерности 2 точечное произведение векторов [a,b] и [c,d] равно ac + bd. Точно так же, в размерности 3, точечное произведение векторов [a,b,c] и [d,e,f] равно ad + be + cf. Например, точечное произведение двух трехмерных векторов [1, 3, -5] и [4, -2, -1] равно

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

Геометрическая интерпретация

В евклидовой геометрии точечное произведение, длина и угол связаны между собой. Для вектора a точечное произведение a - a равно квадрату длины a, или

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}} ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

где ||a|| обозначает длину (величину) a. В более общем случае, если b - другой вектор

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,} $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

где ||a||| и ||b||| обозначают длину a и b, а θ - угол между ними.

Эту формулу можно перестроить для определения величины угла между двумя ненулевыми векторами:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}. $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

Можно также сначала преобразовать векторы в единичные векторы, разделив их на их величину:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

тогда угол θ определяется

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})}. $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

Поскольку косинус 90° равен нулю, точечное произведение двух ортогональных (перпендикулярных) векторов всегда равно нулю. Более того, два вектора можно считать ортогональными тогда и только тогда, когда их точечное произведение равно нулю, и они оба имеют ненулевую длину. Это свойство дает простой метод проверки условия ортогональности.

Иногда эти свойства также используются для определения точечного произведения, особенно в 2 и 3 измерениях; это определение эквивалентно приведенному выше. Для более высоких измерений формула может быть использована для определения понятия угла.

Геометрические свойства основаны на том, что базис является ортонормальным, т.е. состоит из попарно перпендикулярных векторов единичной длины.

Скалярная проекция

Если a и b имеют длину один (т.е. являются единичными векторами), то их точечное произведение просто дает косинус угла между ними.

Если только b - единичный вектор, то точечное произведение a - b дает |a| cos(θ), т.е. величину проекции a на направление b, со знаком минус, если направление противоположное. Это называется скалярной проекцией a на b, или скалярной компонентой a в направлении b (см. рисунок). Это свойство точечного произведения имеет несколько полезных применений (например, см. следующий раздел).

Если ни a, ни b не являются единичными векторами, то величина проекции a на направление b, например, будет равна a - (b / |b|), так как единичный вектор в направлении b равен b / |b|.

Вращение

Вращение ортонормального базиса, в терминах которого представлен вектор a, получается умножением a на матрицу вращения R. Это матричное умножение является просто компактным представлением последовательности точечных произведений.

Например, пусть

B₁ = {x, y, z} и B₂ = {u, v, w} - два различных ортонормальных базиса одного и того же пространства R³ , причем B₂ получается простым вращением B₁ ,
a₁ = (a_x , a_y , a_z ) представляют вектор a в терминах B₁ ,
a₂ = (a_u , a_v , a_w ) представляют тот же вектор в терминах повернутого базиса B₂ ,
u₁ , v₁ , w₁ - повернутые базисные векторы u, v, w, представленные в терминах B₁ .

Затем поворот с B₁ на B₂ выполняется следующим образом:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\{1}\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

Обратите внимание, что матрица вращения R собирается с помощью повернутых базисных векторов u₁ , v₁ , w₁ в качестве ее строк, и эти векторы являются единичными векторами. По определению, Ra₁ состоит из последовательности точечных произведений между каждой из трех строк R и вектором a₁ . Каждое из этих точечных произведений определяет скалярную компоненту a в направлении повернутого базисного вектора (см. предыдущий раздел).

Если₁ является вектором строки, а не вектором столбца, то R должен содержать повернутые базисные векторы в своих столбцах, и должен пост-мультиплицировать₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. } ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

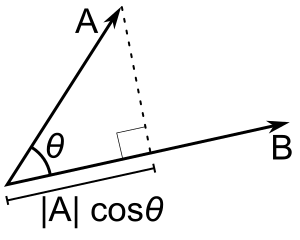
A - B = |A| |B| cos(θ). |A| cos(θ) - это скалярная проекция A на B.

Физика

В физике величина - это скаляр в физическом смысле, т.е. физическая величина, не зависящая от системы координат, выраженная как произведение числового значения и физической единицы, а не просто число. Точечное произведение также является скаляром в этом смысле, задается формулой, не зависит от системы координат. Пример:

Механическая работа - это точечное произведение векторов силы и перемещения.
Магнитный поток - это точечное произведение магнитного поля и вектора площади.
Объемный расход - это точечное произведение векторов скорости жидкости и площади.

Свойства

Если a, b и c - вещественные векторы, а r - скаляр, то справедливы следующие свойства.

Точечное произведение коммутативно:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . } $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

Точечное произведение является дистрибутивным по отношению к векторному сложению:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . } $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

Точечное произведение является билинейным:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). } $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

При умножении на скалярное значение точечное произведение удовлетворяет:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )} $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(последние два свойства вытекают из первых двух).

Два ненулевых вектора a и b перпендикулярны тогда и только тогда, когда a - b = 0.

В отличие от умножения обычных чисел, где если ab = ac, то b всегда равно c, если только a не равно нулю, точечное произведение не подчиняется закону аннулирования:

Если a - b = a - c и a ≠ 0, то по распределительному закону мы можем написать: a - (b - c) = 0; результат выше говорит, что это означает, что a перпендикулярно (b - c), что по-прежнему позволяет (b - c) ≠ 0, а значит b ≠ c.

При условии, что базис ортонормален, точечное произведение инвариантно при изометрических изменениях базиса: поворотах, отражениях и комбинациях, сохраняя фиксированным начало координат. Вышеупомянутая геометрическая интерпретация опирается на это свойство. Другими словами, для ортонормального пространства с любым числом измерений точечное произведение инвариантно при преобразовании координат на основе ортогональной матрицы. Это соответствует следующим двум условиям:

Новый базис снова является ортонормальным (т.е. он ортонормален старому базису).
Новые базисные векторы имеют ту же длину, что и старые (т.е. единичную длину в терминах старого базиса).

Если a и b - функции, то производная a - b равна a' - b + a - b'

Расширение тройного продукта

Это очень полезное тождество (также известное как формула Лагранжа) с участием точечного и перекрестного произведений. Оно записывается как

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )}\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )} $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

которую проще запомнить как "BAC минус CAB", помня о том, какие векторы соединены точками. Эта формула обычно используется для упрощения векторных расчетов в физике.

Доказательство геометрической интерпретации

Рассмотрим элемент R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

Повторное применение теоремы Пифагора дает для его длины |v|

| v | 2 = v 1 2 + v 2 2 + . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

Но это то же самое, что

v ⋅ v = v 1 2 + v 2 2 + . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

поэтому мы заключаем, что взятие точечного произведения вектора v с самим собой дает квадрат длины вектора.

Лемма 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

Теперь рассмотрим два вектора a и b, исходящие из начала координат и разделенные углом θ. Третий вектор c может быть определен как

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,} $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

образуя треугольник со сторонами a, b и c. Согласно закону косинусов, имеем

| c | 2 = | a | 2 + | b | 2 - 2 | a | | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Подставляя точечные произведения для квадратов длин в соответствии с Леммой 1, получаем

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

Но так как c ≡ a - b, мы также имеем

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

которая, согласно распределительному закону, расширяется до

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)

Объединив два c - c уравнения, (1) и (2), получаем

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Вычитание a - a + b - b из обеих сторон и деление на -2 оставляет

a ⋅ b = | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

Обобщение

Внутреннее произведение обобщает точечное произведение на абстрактные векторные пространства и обычно обозначается ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \угольник } $\langle \mathbf {a} \,,\mathbf {b} \rangle$ . В силу геометрической интерпретации точечного произведения норма ||a|| вектора a в таком пространстве внутренних произведений определяется как

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

так, что он обобщает длину, а угол θ между двумя векторами a и b - через

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \угольник }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. } $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

В частности, два вектора считаются ортогональными, если их внутреннее произведение равно нулю

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \угол =0.} $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

Для векторов с комплексными элементами использование данного определения точечного произведения привело бы к совершенно другим геометрическим свойствам. Например, точечное произведение вектора с самим собой может быть произвольным комплексным числом и может быть нулевым без того, чтобы вектор был нулевым вектором; это, в свою очередь, будет иметь серьезные последствия для таких понятий, как длина и угол. Многие геометрические свойства можно сохранить, отказавшись от симметричных и билинейных свойств скалярного произведения, если дать альтернативное определение

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}} $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

где b_i - комплексно сопряженное b_i . Тогда скалярное произведение любого вектора с самим собой является неотрицательным действительным числом, и оно ненулевое, за исключением нулевого вектора. Однако это скалярное произведение не линейно по b (а скорее сопряженно линейно), и скалярное произведение также не симметрично, так как

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

Этот тип скалярного произведения, тем не менее, весьма полезен и приводит к понятиям эрмитовой формы и общего внутреннего произведения пространств.

Внутреннее произведение Фробениуса обобщает точечное произведение на матрицы. Оно определяется как сумма произведений соответствующих компонент двух матриц одинакового размера.

Обобщение на тензоры

Точечное произведение между тензором порядка n и тензором порядка m представляет собой тензор порядка n+m-2. Точечное произведение получается путем умножения и суммирования по одному индексу в обоих тензорах. Если A {\displaystyle \mathbf {A} } $\mathbf {A}$ и B {\displaystyle \mathbf {B} } $\mathbf {B}$ - два тензора с представлением элементов A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} $A_{ij\dots }^{k\ell \dots }$ и B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} $B_{mn\dots }^{p{\dots }i}$ элементы точечного произведения A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } $\mathbf {A} \cdot \mathbf {B}$ даются

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}} $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

Это определение естественным образом сводится к стандартному векторному точечному произведению, когда оно применяется к векторам, и матричному умножению, когда оно применяется к матрицам.

Иногда двойное точечное произведение используется для представления умножения и суммирования по двум индексам. Двойное точечное произведение между двумя тензорами 2-го порядка является скаляром.

Вопросы и ответы

В: Что такое точечное произведение в математике?

О: Точечное произведение - это операция, которая принимает на вход два вектора и возвращает на выходе скалярное число.

В: От чего зависит точечное произведение?

О: Точечное произведение зависит от длины обоих векторов и от угла между ними.

В: Почему название точечного произведения происходит от центрированной точки "-"?

О: Название происходит от центрированной точки "-", которая часто используется для обозначения этой операции.

В: Как альтернативно называется точечное произведение?

О: Альтернативное название - скалярное произведение, что подчеркивает скалярную (а не векторную) природу результата.

В: В чем отличие между точечным и поперечным произведением в трехмерном пространстве?

О: Точечное произведение дает скалярное число в качестве результата, в то время как кросс-продукт дает вектор в качестве результата.

В: Для чего используется точечное произведение в математике?

О: Точечное произведение можно использовать для определения перпендикулярности двух векторов (угол между ними равен 90 градусам) и для проецирования одного вектора на другой.

В: Можно ли использовать точечное произведение в пространствах большей размерности?

О: Да, точечное произведение можно распространить на пространства более высокой размерности, обобщив определение.