Гармонический ряд

В математике гармонический ряд - это дивергентный бесконечный ряд:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{1}{n}=1+{\frac {1}{2}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Расхождение означает, что по мере того, как вы добавляете больше терминов, сумма никогда не перестает увеличиваться. Она не переходит к одному конечному значению.

Бесконечность означает, что вы всегда можете добавить еще один термин. Финального термина в серии не существует.

Ее название происходит от идеи гармоник в музыке: длина волны обертонов вибрирующей струны составляет 1/2, 1/3, 1/4 и т.д. от фундаментальной длины волны струны. Кроме первого термина, каждый термин серии является гармоническим значением терминов по обе стороны от него. Фраза "гармоническое значение" также происходит от музыки.

История

Тот факт, что гармонические серии расходятся, впервые был доказан в 14 веке Николь Оресме, но был забыт. Доказательства были даны в 17 веке Пьетро Менголи, Иоганном Бернулли и Якобом Бернулли.

Архитекторы использовали гармоничные последовательности. В эпоху барокко архитекторы использовали их в пропорциях поэтажных планов, возвышенностей и во взаимоотношениях между архитектурными деталями церквей и дворцов.

Расхождение

Существует несколько известных доказательств расхождения гармонических рядов. Некоторые из них приводятся ниже.

Тест на сравнение

Одним из способов доказать расхождение является сравнение гармонического ряда с другим дивергентным рядом, в котором каждый знаменатель заменяется на следующий по величине - два:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{подпись} &{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots [12pt] \geq {}&1+{\frac {1}{2}+{\frac {1}{\color {red}{\mathbf {4} }}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}++{\frac {1}{\color {red}{\mathbf {8} }}++{\frac {1}{\color {red}{\mathbf {8} }}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}+\cdots \end{aligned}}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Каждый член ряда гармоник больше или равен соответствующему члену второго ряда, и поэтому сумма ряда гармоник должна быть больше или равна сумме второго ряда. Однако сумма второго ряда бесконечна:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}!+!{\frac {1}{4}}\right)+\left({\frac {1}{8}}!+!{\frac}{1}{8}}!+!{\frac}{1}{8}}!+!{\frac {1}{8}\right)+\left({\frac {1}{16}}!+!\cdots !+!!!!{\frac {1}{16}}\right)+\cdots [12pt]={}&1+{\frac {1}{2}+{\frac {1}{2}+{\frac {1}{2}+\frac {1}{2}+\cdots =\infty \end{aligned}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Из этого (по результатам сравнительного теста) следует, что сумма ряда гармоник также должна быть бесконечной. Точнее, сравнение выше доказывает, что

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}\geq 1+{\frac {k}{2}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

на каждое положительное целое число $k$ .

Это доказательство, предложенное Николь Оресме примерно в 1350 году, считается вершиной средневековой математики. Это по-прежнему является стандартным доказательством, преподаваемым на уроках математики сегодня.

Интегральный тест

Можно доказать, что гармонический ряд расходится, сравнивая его сумму с неправильным интегралом. Рассмотрим расположение прямоугольников, показанных на рисунке справа. Каждый прямоугольник имеет ширину 1 единицы и высоту 1/n единиц, поэтому общая площадь бесконечного числа прямоугольников является суммой гармонического ряда:

площадь прямоугольников = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}{\text{rectangles}}\end{array}}=1+{\frac {1}{2}+{\frac {1}{3}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Общая площадь под кривой $y =$ 1/x от 1 до бесконечности задается расходящимся неправильным интегралом:

область под кривой = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}},dx=\infty . } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Так как эта область полностью заключена в прямоугольники, общая площадь прямоугольников также должна быть бесконечной. Это доказывает, что

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac{1}{x},dx=\ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Обобщение этого аргумента известно как интегральный тест.

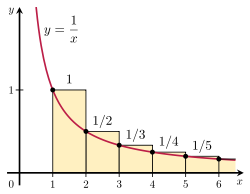
Иллюстрация интегрального теста.

Скорость расхождения

Гармонический ряд расходится очень медленно. Например, сумма первых ¹⁰⁴³ членов меньше 100. Это связано с тем, что частичные суммы ряда имеют логарифмический рост. В частности,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

где γ - константа Эйлера-Маскерони и $εk ~$ 1/2k, которая приближается к 0 по $k$ , переходит в бесконечность. Леонхард Эйлер доказал как это, так и то, что сумма, которая включает только обратные связи праймов, также расходится, то есть:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}={\frac {1}{2}+{\frac {1}{3}+{\frac {1}{5}}+{\frac {1}{7}+{\frac {1}{11}}+{\frac {1}{13}+{\frac {1}{17}}+\cdots =\infty . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Частичные суммы

Первые тридцать гармонических чисел
$n$	Частичная сумма гармонического ряда, $Hn$
$n$	выраженный в виде дроби		десятичная дробь	относительный размер
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Конечные частичные суммы расходящихся гармонических рядов,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

называются гармоническими числами.

Разница между $Hn$ и $ln n$ сходится с константой Эйлера-Машерони. Разница между любыми двумя гармоническими числами никогда не является целым числом. Никакие гармонические числа не являются целыми числами, за исключением $H1 = 1$ .

Связанная серия

Серия переменных гармоник

Серия

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}=1-{\frac {1}{2}}+{\frac {1}{3}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

известен как серия переменных гармоник. Эта серия сходится с помощью теста переменной серии. В частности, сумма равна натуральному логарифму 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Чередующийся ряд гармоник, хотя и условно сходящийся, не является абсолютно сходящимся: если члены ряда систематически перестраиваются, то в целом сумма становится иной и, в зависимости от перестройки, возможно, даже бесконечной.

Формула серии переменных гармоник является особым случаем серии Меркатора, серии Тейлора для натурального логарифма.

Связанная серия может быть получена из серии Тейлора для арткангента:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}+{\frac {1}{5}-{\frac {1}{7}+\cdots ={\frac {\pi }{4}}. } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Это известно как серия "Лейбниц".

Серия общей гармоники

Общий гармонический ряд имеет форму

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

где $a \neq 0$ и $b$ - вещественные числа, а b/a - не ноль и не отрицательное целое число.

При испытании на сравнение предельных значений с сериями гармоник все серии общих гармоник также расходятся.

$p-серии$

Обобщением гармонического ряда является $p-серии$ (или гипергармонический ряд), определяемый как

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

для любого вещественного числа $p$ . При $p = 1$ , $p-серия$ является гармонической серией, которая расходится. Либо интегральный тест, либо тест на конденсацию Коши показывает, что $p-серии$ сходятся для всех $p > 1 (в этом случае их$ называют сверхгармоническими рядами) и расходятся для всех p ≤ $1.$ Если $p > 1$ , то суммой p-серии является ζ( $p), т.е.$ функция дзеты Римана, оцениваемая при p.

Проблема нахождения суммы для $p = 2$ называется Базельской задачей; Леонхард Эйлер показал, что это ^π2/6. Значение суммы для $p = 3 называется$ константой Апери, поскольку Роже Апери доказал, что это иррациональное число.

ln-серии

К $p-серии$ относится ln-серии, определяемая как

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

для любого положительного вещественного числа $p$ . Это может быть показано интегральным тестом, который расходится для $p \leq 1$ , но сходится для всех $p > 1.$

$φ-серии$

Для любой выпуклой, реально оцененной функции $φ$ такой, чтобы

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}\right)}{\varphi (u)}}<{\frac {1}{2}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

серия

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

сходится. ^[]

Случайные серии гармоник

Случайный ряд гармоник

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

где $sn$ являются независимыми, идентично распределенными случайными переменными, принимающими значения +1 и -1 с равной вероятностью 1/2, является известным примером в теории вероятностей для ряда случайных переменных, сходящихся с вероятностью 1. Факт такого сходства является легким следствием либо теорем Колмогорова трех серий, либо близкородственным Колмогорову максимальным неравенством. Байрон Шмуланд из Университета Альберты дополнительно изучил свойства случайного ряда гармоник и показал, что сходящийся ряд является случайной переменной с некоторыми интересными свойствами. В частности, функция плотности вероятности этой случайной величины, оцененная при +2 или -2, принимает значение 0,124999999999999999999999999999764..., отличающееся от 1/8 менее чем на 10-42. В работе Шмуланда объясняется, почему эта вероятность так близка к 1/8, но не совсем точна. Точное значение этой вероятности дает бесконечный косинусный интеграл $С2$ , разделенный на π.

Испорченный ряд гармоник

Обедненная гармоническая серия, в которой все термины, в которых цифра 9 появляется в любом месте знаменателя, удалены, может быть показана как сходящаяся, и ее значение меньше 80. Фактически, при удалении всех терминов, содержащих какую-либо определенную строку цифр (в любом основании), серия сходится.

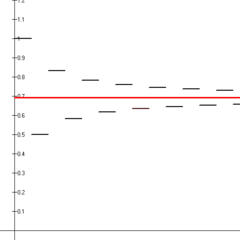
Первые четырнадцать частичных сумм чередующихся гармонических рядов (сегменты черной линии) показаны сходящимися с натуральным логарифмом 2 (красная линия).

Заявления

Серия гармоник может быть интуитивно понятной. Это объясняется тем, что это расходящаяся серия, несмотря на то, что сроки серии становятся меньше и идут к нулю. Расхождение ряда гармоник является источником некоторых парадоксов.

"Червь на резинке". Предположим, что червь ползает по бесконечно упругой однометровой резинке одновременно с равномерно натянутой. Если червь будет двигаться со скоростью 1 см в минуту, а лента будет растягиваться на 1 метр в минуту, достигнет ли он когда-нибудь конца резинового кольца? Ответ интуитивно понятен: "Да", поскольку через $n$ минут отношение пройденного червем расстояния к общей длине резинки составляет

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Поскольку серия становится произвольно большой по мере того, как $n$ становится больше, в конце концов это соотношение должно превысить 1, что означает, что червь достигает конца резиновой ленты. Однако значение $n$ , при котором это происходит, должно быть чрезвычайно большим: примерно e100, число, превышающее ¹⁰⁴³ минуты (1037 лет). Несмотря на то, что гармонический ряд действительно расходится, он делает это очень медленно.

Проблема с "Джипом" спрашивает, сколько всего топлива требуется автомобилю с ограниченной грузоподъемностью, чтобы пересечь пустыню, в результате чего топливо падает по маршруту. Расстояние, которое автомобиль может пройти с заданным количеством топлива, связано с частичными суммами гармонических серий, которые растут логарифмически. Таким образом, требуемое топливо возрастает экспоненциально с увеличением желаемого расстояния.

Проблема блочного стекания: при наличии коллекции одинаковых домино можно укладывать их по краю стола так, чтобы они свисали по краю стола, не падая. Противоинтуитивный результат заключается в том, что их можно сложить таким образом, чтобы свесы были как можно больше. То есть, при условии, что будет достаточно домино.

Пловец, который быстрее плывет каждый раз, когда касается стены бассейна. Пловец начинает пересекать 10-метровый бассейн со скоростью 2 м/с, а с каждым пересечением к скорости добавляются еще 2 м/с. Теоретически, скорость пловца неограниченна, но количество переходов через бассейн, необходимое для того, чтобы добраться до этой скорости, становится очень большим; например, чтобы добраться до скорости света (игнорируя особую относительность), пловцу необходимо пересечь бассейн 150 миллионов раз. В отличие от этого большого числа, время, необходимое для достижения заданной скорости, зависит от суммы серий при любом заданном количестве пересечений бассейна:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Расчет суммы показывает, что время, необходимое для достижения скорости света, составляет всего 97 секунд.

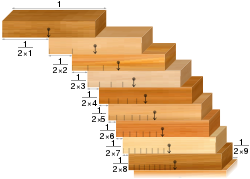
Проблема укладки блоков: блоки, выровненные в соответствии с серией гармоник, перекрывают расщелины любой ширины.

Связанные страницы

Гармоническая прогрессия
Список сумм взаимных расчетов

Вопросы и ответы

В: Что такое гармонический ряд?

О: Гармонический ряд - это бесконечный расходящийся ряд, в котором каждый член равен 1, деленной на его положение в последовательности.

В: Что значит для ряда быть расходящимся?

О: Дивергентность означает, что по мере добавления новых членов сумма не перестает увеличиваться и не стремится к одному конечному значению.

В: Что означает для ряда быть бесконечным?

О: Бесконечный означает, что Вы всегда можете добавить еще один член, и у ряда нет конечного члена.

В: Откуда взялось название этой серии?

О: Название этой серии происходит от идеи гармоник в музыке, где длины волн обертонов составляют 1/2, 1/3, 1/4 и т.д. от основной длины волны струны.

В: Что такое среднее гармоническое?

О: Среднее гармоническое - это когда каждый член последовательности равен среднему гармоническому соседних членов. Это выражение также пришло из музыки.

В: Как вычислить каждый член этой последовательности?

О: Каждый член этой последовательности можно вычислить, разделив единицу на его положение в последовательности (1/n).