Поверхностный интеграл

В математике поверхностный интеграл - это определенный интеграл, взятый по поверхности (которая может быть кривой, заданной в пространстве). Подобно тому, как линейный интеграл работает с одним измерением или одной переменной, поверхностный интеграл можно рассматривать как двойной интеграл по двум измерениям. Задавая поверхность, можно интегрировать по ее скалярным полям (то есть функциям, которые возвращают числа как значения) и векторным полям (то есть функциям, которые возвращают векторы как значения).

Поверхностные интегралы находят применение в физике, особенно в классической теории электромагнетизма.

Определение поверхностного интеграла основывается на разбиении поверхности на мелкие элементы поверхности.

Иллюстрация одного элемента поверхности. Эти элементы делаются бесконечно малыми с помощью процесса ограничения, чтобы приблизить поверхность.

Поверхностные интегралы скалярных полей

Рассмотрим поверхность S, на которой определено скалярное поле f. Если считать, что S состоит из некоторого материала, и для каждого x в S число f(x) является плотностью материала в точке x, то поверхностный интеграл f по S - это масса на единицу толщины S. (Это верно только в том случае, если поверхность представляет собой бесконечно тонкую оболочку.) Один из подходов к вычислению поверхностного интеграла состоит в том, чтобы разделить поверхность на множество очень маленьких частей, предположить, что на каждой части плотность приблизительно постоянна, найти массу на единицу толщины каждой части путем умножения плотности части на ее площадь, а затем сложить полученные числа, чтобы найти общую массу на единицу толщины S.

Чтобы найти явную формулу для поверхностного интеграла, математики параметризуют S, рассматривая на S систему криволинейных координат, таких как широта и долгота на сфере. Пусть такой параметризацией будет x(s, t), где (s, t) изменяется в некоторой области T на плоскости. Тогда поверхностный интеграл дается следующим образом

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt} $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

где выражение между столбиками в правой части - величина перекрестного произведения частных производных x(s, t).

Например, чтобы найти площадь поверхности некоторой общей функциональной формы, скажем z = f ( x , y ) {\displaystyle z=f\,(x,y)} $z=f\,(x,y)$ , мы имеем

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy} $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

где r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ . Так что ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))} ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ , и ∂ r ∂ y = ( 0, 1, f y ( x, y ) ) {\displaystyle {\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ . Итак,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}}}} ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

которая является формулой, используемой для площади поверхности общей функциональной формы. Вектор во второй строке выше можно распознать как вектор нормали к поверхности.

Обратите внимание, что из-за наличия перекрестного произведения приведенные выше формулы работают только для поверхностей, вписанных в трехмерное пространство.

Поверхностные интегралы векторных полей

Рассмотрим векторное поле v на S, то есть для каждого x в S, v(x) является вектором.

Поверхностный интеграл может быть определен по компонентам в соответствии с определением поверхностного интеграла скалярного поля; результатом является вектор. Например, это применимо к электрическому полю в некоторой фиксированной точке, обусловленному электрически заряженной поверхностью, или к силе тяжести в некоторой фиксированной точке, обусловленной листом материала. Также можно рассчитать магнитный поток через поверхность.

В качестве альтернативы математики могут интегрировать нормальную составляющую векторного поля; результатом является скаляр. В качестве примера можно привести жидкость, протекающую через S, так что v(x) определяет скорость жидкости в точке x. Поток определяется как количество жидкости, протекающей через S за единицу времени.

Из этой иллюстрации следует, что если векторное поле направлено по касательной к S в каждой точке, то поток равен нулю, поскольку жидкость течет параллельно S, но не втекает и не вытекает. Из этого также следует, что если v течет не только вдоль S, то есть если v имеет как тангенциальную, так и нормальную составляющую, то только нормальная составляющая вносит вклад в поток. Исходя из этих рассуждений, чтобы найти поток, нужно взять точечное произведение v с нормалью единичной поверхности к S в каждой точке, что даст нам скалярное поле, и проинтегрировать полученное поле, как указано выше. Это дает формулу

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt. } $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

Перекрестное произведение в правой части этого выражения является нормалью поверхности, определяемой параметризацией.

Эта формула определяет интеграл слева (обратите внимание на точку и векторную нотацию для элемента поверхности).

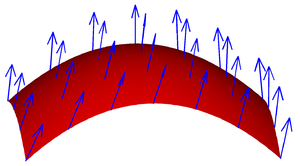
Векторное поле на поверхности.

Теоремы, связанные с поверхностными интегралами

С помощью дифференциальной геометрии и векторного исчисления можно получить различные полезные результаты для поверхностных интегралов, например, теорему о расходимости и ее обобщение - теорему Стокса.

Дополнительные вопросы

Изменение параметризации

В приведенном выше обсуждении поверхностный интеграл определялся с помощью параметризации поверхности S. У данной поверхности может быть несколько параметризаций. Например, когда местоположение Северного и Южного полюсов перемещается по сфере, широта и долгота изменяются для всех точек на сфере. Естественный вопрос заключается в том, зависит ли определение поверхностного интеграла от выбранной параметризации. Для интегралов скалярных полей ответ на этот вопрос прост: значение поверхностного интеграла будет одинаковым независимо от того, какую параметризацию использовать.

Интегралы от векторных полей сложнее, поскольку в них участвует нормаль поверхности. Математики доказали, что при двух параметризациях одной и той же поверхности, нормали которой направлены в одну сторону, обе параметризации дают одно и то же значение поверхностного интеграла. Если же нормали этих параметризаций направлены в противоположные стороны, то значение поверхностного интеграла, полученное с помощью одной параметризации, равно отрицательному значению интеграла, полученного с помощью другой параметризации. Из этого следует, что при наличии поверхности нам не нужно придерживаться какой-либо единственной параметризации; но при интегрировании векторных полей нам нужно заранее решить, в какую сторону будет направлена нормаль, а затем выбрать любую параметризацию, соответствующую этому направлению.

Параметризация работает на части поверхности

Другая проблема заключается в том, что иногда поверхности не имеют параметризаций, которые охватывают всю поверхность; это верно, например, для поверхности цилиндра (конечной высоты). Очевидное решение - разбить поверхность на несколько частей, вычислить поверхностный интеграл по каждой части, а затем сложить их все. Это действительно так, но при интегрировании векторных полей необходимо снова тщательно выбирать вектор нормали для каждой части поверхности, чтобы при соединении частей вместе результаты совпадали. Для цилиндра это означает, что если мы решили, что для боковой области нормаль будет направлена от тела, то для верхней и нижней круговых частей нормаль также должна быть направлена от тела.

Несоответствие нормалей поверхности

Наконец, существуют поверхности, которые не имеют поверхностной нормали в каждой точке с последовательным результатом (например, полоса Мёбиуса). Если такую поверхность разделить на части, для каждой части выбрать параметризацию и соответствующую поверхностную нормаль, и собрать части вместе, то нормальные векторы, исходящие от разных частей, не могут быть согласованы. Это означает, что на каком-то стыке двух кусков нормали будут направлены в противоположные стороны. Такая поверхность называется неориентируемой. Векторные поля не могут быть проинтегрированы на неориентируемых поверхностях.